流出解析

流出モデル設定の基礎

流出現象の分析と総合

流出解析とは、流出現象に関与する個々の現象の物理的あるいは数理的（確率統計的なものを含む）な機構を明らかにするとともに、それら相互の関係を明確にしたうえで、流域における全体としての流出現象を論理的に記述することであって、図-1に示した流出システムの分析と総合がその基礎となります。

すでにみたように、流出システムは時間的にも場所的にも、さらに流れの機構という点でも性質を異にする種々の要素から成るきわめて多次元の複雑なシステムであって、その特性にもいろいろな側面が現れます。したがってその分析と総合にあたっては、検討の対象とする事象、現象をまず明確にしておくことが肝要です。

例えば、豪雨による出水といっても、単に河川のある地点で生じる最大流量や最大水位状態とその生起時刻だけを知ればよい場合もあれば、洪水の制御問題のように、洪水波形の時間的、場合によっては場所的分布を知らなければならないこともあります。また水資源計画などでは何か月〜年といった長期にわたる流出の状況が問題となります。

このように、同じ流出現象を対象とするといっても、対象とする問題の違いに応じて、前記のシステム（図-1）のうちで焦点を合せるべき現象、特性が異なり、その分析、総合の仕方について最適なものが選ばれなければなりません。さらに、その評価の基準も異なることに注意しなければなりません。

流出モデル

流出モデルとは、流域内部における流出現象の挙動、とりわけその原因としての降雨と結果としての流出との関係を論理的に表現するものの総称です。流出現象を普遍的に表現するためには、図-1のサブシステムの個々の流れ、個々の現象の構造機構を正しく記述することが基礎となります。その場合、流出現象が流域内部での物理的、力学的な流れとして起っていることに焦点を合せ、各種現象の物理的な法則性を基礎として構成した流出モデルを物理モデルといいます。

また、図-1のサブモデルでは、一段上位のサブモデルの出力を入力として受けたのち、ある種の変換が行われて次のサブシステムに出力を出すという構造をしています。そして、全システムでは降雨が入力、流出が出力となっています。このような観点に立って、トータルシステムあるいは主要なサブシステムを入力から出力への応答系として記述しようというのが応答モデルと呼ばれるものです。

一方、降雨や流域またそれらの状態、流域内部での流れのそれぞれには不確定な要素が多く含まれています。したがって、当然、確率統計的な記述（確率統計モデル）もされ、また種々の現象の数学的な相互関連を基礎とする数理モデルなども用いられています。これらの分類はモデルの主要部の扱いいかんによるもので、実際には、あるサブシステムあるいはいくつかのサブシステムは物理的に表現し、他の部分は統計的に扱うなどいろいろな組合せが用いられていることはいうまでもありません。

上記とは違った観点からの分類もあります。すなわち、モデルが流れ現象の流域内部での場所的、時間的分布の両者を扱おうというとき分布系モデルと呼ばれ、場所的分布は扱わず、流域全体としての水文量の時間的挙動のみに注目したものを集中系モデルと呼びます。また、どのようなモデルでも、モデル表現の主要部の数理構造が線形であるか否かによって、線形モデル、非線形モデルと分類されます。

現象の分析と洞察に基づいて構造が決定された流出モデルを実際の河川に応用するに際しては、通常はモデルの同定と検証のプロセスが必要となります。同定とは実際の現象・観測値を十分の精度で再現するようにモデルパラメータを決定することであり、検証とはそうして定められたモデルが普遍性をもちうるか否かを確かめることです。したがって、同定に用いられる観測値、検証に用いられる観測値は同一のものであってはならないことはいうまでもなく、検証の結果の良否も単に外見上・計算上の判断でなく、その内容、意味をよく吟味する必要があります。

複雑な流出現象に含まれる諸要素、諸パラメータ相互の論理構造を明確にしつつ、できる限り数少ない情報、数少ないパラメータで流出モデルを組み立てる方向を流出解析の総合化と呼んでいます。流出モデルに組み込まれる構造はある確かな論理に基づいたものに限定されるべきであって、未知の部分はブラックボックスとして今後の検討に残し、特別な意味づけはしない方が賢明です。

流出現象のサンプリング

流出現象は流域の最小単位の場での現象が基礎となって起っています。しかしながら、実際の流域というスケールでの現象を扱うに際しては、きわめて小さい個々の山腹や河谷を一つ一つ扱うのは得策ではありません。むしろ、最小単位のある程度の集合体としての流域を単位流域として扱う方が好ましいです。どの程度の場を単位として扱うかは、解析の対象とする現象の規模について、降雨と、流域内部での流下過程で受ける流れの変換、平均化の程度に応じて定められるべきものです。

時間的・空間的にある集中、あるいは偏りをもった分布として地上に達した降雨は、流域内の流下過程での力学的・統計的変換を通じて平均化、平滑化されつつ流域末端での流出を生みます。したがって、流域末端での流出流量という現象に対して大きな変化や影響を及ぼさない程度の降雨の場所的・時間的分布の偏りの詳細は無視してさしつかえありません。

流域の扱いについても同様です。すなわち、山腹長、勾配、地質、地被状態などの分布は複雑であるとはいえ、それらの影響が相殺し、流出過程で十分平均化・平滑化されてしまう程度の広がりの場は、一様な流域として考えてよいです。複雑な流出現象をどの程度の時間的・場所的（面積的）基準単位で検討するべきかについては、まだ確たる定説はありませんが、流出モデルの構成にあたって十分留意しなければなりません。

水収支

水収支は、対象とする体積・期間についての水の質量（量）の保存則を記述するものである。したがって、水収支を考えるにあたっては対象とする体積と時間をまず明確にしておかなければなりません。

図-3.1：流出のシステム

図-3.1は1つの流域を地表システムと地下システムの2つの体積に分割した概念図であって、水収支の基本式は、

地表システムについて

$$\Delta S_s=P+ (D_1-D_2)-E-F_1 \tag{3.1}$$

地下システムについて

$$\Delta S_g=F_1+ (G_1-G_2)-F_2 \tag{3.2}$$

トータルシステムについて

$$\Delta S_s + \Delta S_g = P+ (D_1-D_2)+(G_1-G_2)-E-F_2 \tag{3.3}$$

と記されます。

ここに、$P$は降水量、$D_1(D_2)$は地表水としての流入（出）量、$G_1(G_2)$は地下水の流入（出）量、$dS_s, dS_g$は地表および地下での貯留量増分、$F_1, F_2$はそれぞれ地表システムより地下システムへ、地下システムよりさらに下方への流去量、$E$は蒸発量で、これらの量は対象とする領域体積・時間での水の量です。

実際に水収支を確立するためには、その目的に応じて対象とする体積をできるだけ境界条件が判明している体積として選定することが望ましいです。また、流域における水の挙動には種々の時間スケールのものがあるので、基本的には対象とする現象のスケールに合った時間単位を選定する必要があります。

さらに、対象とする期間を例えば降雨継続時間、無降雨期間と種々変化させつつ水収支を検討すると、対象領域内での水収支の実態を把握するためのより詳しい情報が得られることが多いです。なお、上記の式（3.1）〜（3.3）の個々の量の評価には第2章で記した諸関係等が応用されます。

流出成分の分離と有効降雨

有効降雨と流出成分

前述したように、河川の流出量にはいくつかの流出成分があります。降雨のうち、対象とする流出成分になる降雨分を有効降雨といい、流出成分にならない降雨成分を損失降雨といいます。

長期流出解析の場合には間接・直接雨流出成分が対象とされ、損失降雨は蒸発散が大部分を占めます。洪水流出解析では、一般に直接流出成分が対象とされます。この場合、植物による遮断、窪地貯留、土層中の水分保留および地下水貯留が損失降雨となります。一連の洪水に対する総有効雨量は、直接流出成分の総量に等しいです。

種々の水文指標と関連づけて総有効雨量を推定しようとするいくつかの方法があります。簡便なため最もよく用いられるのは、累加雨量ー累加損失量曲線です。これは多くの出水記録について総雨量から成分分離によって求めた直接流出量を差し引いた量（すなわち損失雨量）を総雨量に対してプロットして得られる関係であり（図-3.3）、累加雨量の増加に伴い損失雨量の割合が漸減するという考えに基づいています。

図-3.3：累加雨量 - 累加損失量曲線

流域の乾湿を表わす指標APIと降雨量、降雨継続時間、年週別番号などをパラメータとして有効雨量を推定する共軸相関法、初期流量をパラメータとして降雨量と有効雨量を求める方法、流出率を初期流量と平均降雨強度の関数で表わす方法などが提案されています。

流出成分の分離

実測ハイドログラフに対して直接流出成分と間接流出成分を分離することを流出成分の分離といいます。図-3.2は、その代表的な方法を示したものです。

図-3.2：直接流量の分離法

a. 水平分離法：ハイドログラフの立上り点Aから水平線A-A'を引き、その上部を直接流出、下部を間接流出とします。出水期間中の間接流出量の増減を無視している点で必ずしも合理的ではありませんが、間接流出量は直接流出量に比べて通常2オーダ程度小さいことが、こうした近似を可能にしています。

b. 流量の指数低減性を利用する方法：ハイドログラフの低減部は片対数紙に描くと、2本または3本の直線の和で近似できます。2本の場合はその折点、3本の場合は第2の折点を早い中間流出の終了時点（直接流出の終了時点）とみなしてB点を決めます。A点、B点を直線で結ぶことにより分離します。

c. 間接流出の時間変化を見積る方法：A点と直接流出終了点Bがわかったとしても、両点間で間接流出成分がいかなる変化をしているかが厳密には問題になります。これを的確に評価する方法はまだ確立されていませんが、次の2つの推定法が提案されています。一つは図中の線ACBであり、出水のピーク時までは出水前の地下水流出の低減状態が続くものとしてその延長線上にC点を決め、その後はB点に向かつて間接流出が増加するという近似です。もう一つは、曲線ADBのように、出水期間のある時点で間接流出も上昇しピークを形成する場合です。間接流出の立上り部の見積り等が難しいので、現状では厳密な推定法はありませんが、便宜的な方法として、B点以後の低減状態を降雨終了時刻Dまで逆に延長し、AとDとを直線で結ぶ分離法などが提案されています。。

有効降雨の時間配分

直接流出を対象とする短期流出モデルでは、一般に有効降雨の時間配分が問題となります。有効降雨時系列は、観測降雨時系列から損失降雨時系列を差し引くことによって求められますが、通常これには、初期損失の算定と初期損失後の損失降雨（裏をかえせば有効降雨）の時間変化の算定の2つの段階があります。

初期損失は、直接流出の発生時点以前の降雨と定義され、樹草などによる遮断、土中の水分保留、窪地貯留などを合せたものです。前述のAPIや初期流量などの流域の乾湿を表わす指標と関連づけて初期損失量の推定が行われます。わが国での研究例では、立神が初期流量と関連づけて提案した次式があります。

$$I_1=-\alpha Q_i+C \tag{3.4}$$

ここに、$I_1$は初期損失（mm）、$Q_i$は初期地下水流出量（m$^3$/s）、$\alpha, C$は流域の特性と季節によって定まる定数。

直接流出発生後の損失降雨の時間変化の推定に対して、累加雨量一累加損失量曲線を利用することができます。

得られた累加雨量$R$と累加損失量$R_L$の関係を図-3.3に示すように$R_L=f(R)$とすると、各時刻の損失降雨強度$r_l$と有効降雨強度$r_e$は次式で求めることができます。

$$r_l(t)={f\left(\sum_{t=0}^{t}r(t)\right)-f\left(\sum_{t=0}^{t-\Delta t}r(t)\right)}\bigg/{\Delta t} \tag{3.5}$$

$$r_e(t)=r(t)-r_l(t) \tag{3.6}$$

ここに、$r(t)$は観測降雨強度、$t$は降雨開始時を0とした時間、$\Delta t$は単位時間です。この場合、初期損失は降雨の初期における$R=R_L$の部分で表現されています。

Hortonの浸透能式（式（2.10））を用いて損失雨量の時間配分を推定する方法も提案されています。また、簡便法として、実測降雨時系列に流出率（=直接流出量/総雨量）を乗じて有効降雨時系列とする方法、初期損失後は損失雨量を一定とする方法なども用いられます。

有効降雨の評価法には、従来流出モデルごとに特有な定式化がなされる傾向が強いですが、雨水の保留・浸透あるいは蒸発散機構の解明という立場からの研究が最近では盛んになっています。有効降雨の評価に直接結びつく研究として、流量時系列に数値フィルタとARモデルを適用することにより、各流出成分に対する有効降雨時系列を逆推定する手法の提案および、それら成分雨量と流出寄与域の消長との関連づけの試みなどがあります。また、洪水到達時間内について流出率を定義し、降雨特性による有効降雨強度の変動を検討した研究もあります。

短期流出

合理式

合理式は、洪水ピーク流量を算定するのに古くから用いられてきました。特に中小河川、下水道など洪水調節施設を含まない排水計画では、流出量の推定に合理式が用いられることが多いです。

合理式は、次式で表現されます。

Q_p \biggl( = \frac{1}{3.6}\cdot r_e \cdot A \biggr）= \frac{1}{3.6}\cdot f_p \cdot r_e \cdot A \tag{3.7}

ここに、$Q_p$は洪水ピークの流量（m$^3$/s）、$r_e$は洪水到達時間内の最大平均有効降雨強度で$r_e=f_p \dot r$、$f_p$はピーク流出係数、$r$は洪水到達時間内の最大平均降雨強度（mm/h）、$A$は流域面積（$km^2$）です。

式（3.7）は連続式ですが、「洪水到達時間内の最大平均降雨強度」という表現の中に流域における集水状態、すなわち、運動の概念を含んでいます。合理式の適用範囲は、豪雨の面積スケール40km$^2$程度以下の流域と考えられますが、流域と降雨条件が一様とみなされる場合にはより大きな流域にも適用されます。$Q_p$を求めるには、洪水到達時間とその時間内の平均降雨強度およびピーク流出係数が必要です。

洪水到達時間を推定する方法として、古くは流路勾配と洪水到達速度を関連づけたいわゆるクラーヘンの表がありますが、土木研究所は全国流出試験地調査により収集した資料を整理して次式を提案しました。

$$\text{都市流域} T_p=2.40 \times 10^{-4} (L/\sqrt{S})^{0.7} \tag{3.8}$$

$$\text{自然流域} T_p=1.67 \times 10^{-3} (L/\sqrt{S})^{0.7} \tag{3.9}$$

ここに、$T_p$は洪水到達時間（h）、$L$は流域最遠点から流量計算地点までの流路長（m）、$S$は平均流路勾配で、ここでは、洪水到達時間は降雨ピークから流出ピークまでの時間の2倍と定義し、Manning型平均流速を想定して$T_p$と$L/\sqrt{S}$を関連づけています。

一方、kinematic wave理論では、到達時間は「流域斜面上流端の雨水の擾乱が下流端に伝播する時間」と定義され、石原・高樟は矩形斜面上の表面流に対して次の関係を導きました。

$$T_p = t_p - \tau_p = KL^p/{r_e}^{1-p} \tag{3.10}$$

$$\gamma_e(\tau_p) = \gamma_(t_p) \tag{3.11}$$

ここに、$T_p$は洪水到達時間、$\tau_p$はピーク流量を発生する特性曲線の上流端での出発時刻、$t_p$はその特性曲線の下流端への到達時刻、$L$は斜面長、$r_e$は$t_0 \sim t_p$間の平均有効降雨強度、$K,p$は水深と流量の関係を$h=Kq^p$と表わしたときの係数です。

角屋らは、式（3.10）に河道長と流域面積の関係に関する地形則を導入することにより、次の洪水到達時間推定式を提案しました。

$$T_p = C \cdot A^{0.22} \cdot {r_e}^{-0.35} \tag{3.12}$$

ここに、$T_p$は（min）、$A$は流域面積（km$^2$）、$r_e$は（mm/h）、$C$は流域特性を表わす係数で、丘陵山林地流域：290、粗造成宅地：90〜120、放牧地・ゴルフ場：190〜200、市街化地域：60〜90、の値が提示されています。式（3.12）では、降雨規模に応じて到達時間が変化するという特性を表現している点が特徴です。

ピーク流出係数$f_p$は、分野あるいは使用目的に応じていろいろなものが提示されています。例えば、流域の大まかな特性に対応させて概数値を与えた物部の表、防災調整池の設計に際して開発の程度に応じて与えられたもの、表土層の地質等との対応で分類したもの、などがあります。

合理式は、確率降雨強度曲線（4.4参照）と組み合せることによって、確率ピーク流量の算定に用いられます。すなわち、洪水到達時間$T_p$が定まれば、各確率年に対する継続時間降雨強度関係式を用いて、所要の発生確率をもつ$T_p$時間内の最大平均降雨強度が得られ、式（3.7）より所要の確率ピーク流量が計算できます。ただし、到達時間式として式（3.12）を使う場合には$T_p$が独立には求まらないので、所要の確率降雨強度式と連立させることにより$T_p$と$r_e$を定めなければなりません。

単位図法

単位図法は狭義には、1932年Shermanが提案した有効降雨から直接流出波形を推定する線形応答モデルに対して付された呼称ですが、ここでは、その後様々な形で発展した線形応答モデルを広義に単位図法と総称して議論します。

一般に、入力$r_e(t)$と出力$q(t)$の対応に線形性と定常性が保たれる応答モデルは、次の3種の形式によって表わすことができます。

たたみ込み積分による表現

$$q(t)=\int_0^\infty r_e (t-\tau)h(\tau) (d\tau) ,\qquad \int_0^\infty h(\tau)d\tau = 1 \tag{3.13}$$

あるいは、これを離散表示して、

$$q(t)=\sum_{j=0}^n r_e(t-j \Delta t)h(j \Delta t) \Delta t \qquad (3.13')$$

線形常微分方程式による表現

$$k_m \frac{d^m q}{dt^m} + k_{m-1} \frac{d^{m-1} q}{dt^{m-1}} + \cdots + k_1 \frac{dq}{dt} + k_0 q = r_e(t) \qquad (3.14)$$

ARMA形式による表現

$$q_t = (a_1 q_{t-1} + a_2 q_{t-2} + \cdots + a_i q_{t-i}) + (b_0 r_{e,t} + b_1 r_{e,t-1} + \cdots + b_j r_{e,t-j}) \qquad (3.15)$$

降雨ー流出系の場合、$q(t), q, q_t$：時刻$t$における直接流出高、$r_e(t)$：有効降雨強度、$h(\tau), h(j \Delta t)$：単位図あるいは応答関数、$\Delta t$：単位時間、$n \Delta t$：単位図の基底長、$k, a, b$：係数です。

式（3.13）と式（3.13'）がShermanが提案した単位図法の数学的表現形式です。式（3.14）は一般的な表現で、$m$個の線形貯水池を直列につないだ場合の入力と出力の関係もこの式で表わせます。式（3.15）は、入力と出力の関係を自己回帰移動平均（Auto-Regressive Moving Average、略してARMA）過程として表現したものです。これら3つの表現形式は相互に関係があり、式（3.13）の単位図$h(\tau)$は、式（3.14）の積分変換によって定数$k$で、また、離散表示した単位図$h(j \Delta t)$は式（3.15）の係数$a, b$で表わすことができます。

降雨ー流量の実測資料を用いて単位図を定める、言い換えればそれぞれの定数値を定める方法には、式（3.13'）に基づき代数的試算によって求める方法、最小2乗法を用いる方法、式（3.13）の積分変換などによる方法、時系列解析手法を用いる方法、などがあります。また、地形特性と関連づけた集中面積図から単位図を定める方法もあります。

実測資料によらず、地形特性等から単位図を構成しようとしたものを総合単位図といい、Snyder、中安、石原らの方法などがあります。

わが国では、単位図の線形仮定が成立しない場合が多いこと、したがって、降雨規模別に単位図を変える必要があることが指摘されてきました。また、単位図の物理的意義を斜面長の分布との関係で明らかにした近年の研究が注目されます。

等しい定数$K$をもつ$n$個の線形貯水池を直列につないだNashのモデルは、式（3.14）の特別な場合であり、瞬時の単位入力に対する出力、すなわち、単位図$h(t)$を次のように記しています。

$$h(t) = \frac{1}{K^n \Gamma(n)} t^{n-1} e^{-t/K} \qquad (3.16)$$

ここに、$\Gamma(n)$はガンマ関数です。$n=1$の場合が柴原、菅原・丸山のモデルに、$n=2$の場合が佐藤らの流出関数法と呼ばれるモデルに、$n$を$(n+1)$ に置き換えたものが石原・高瀬の流出関数モデルに相当します。

ARMA形式（3.15）を後進演算子を用いて書き直し整理すると式（3.13'）の表現形式が導かれます。

式（3.15）の係数$b$が$b_0$を除いてすべて0で、$r_e(t)$が白色雑音と考えられる場合、式（3.15）はARモデルとなります。

日野らは、低減特性を基に定めた数値フィルタにより流量時系列を各流出成分に分離し、それぞれの流出成分がARモデルで表現できる、言い換えれば、線形系とみなせることを見出し、降雨ー流出系の非線形性は、降雨の各流出成分系への分離則の非線形性にあるとしています。

貯留関数法

流域を集中系とみなし、そこでの連続式と流出量ー貯留量関係式（これを貯留関数と呼ぶ、2.8.2参照）を用いて流出量を追跡する方法を一般に貯留関数法といいます。

$$\frac{dS}{dt} = r_e - q \tag{3.17}$$

$$q = f(S) \tag{3.18}$$

ここに、$S$は流域上の雨水貯留高、$r_e$は有効降雨強度、$q$は直接流出高です。

貯留関数としては、基本的には次の3種のモデルが提案されています。

$$\text{木村のモデル } S = Kq^p \tag{3.19}$$

$$\text{Prasadのモデル } S = K_1 q^{p_1} + K_2 \frac{dq}{dt} \tag{3.20}$$

$$\text{星・山岡のモデル } S = K_1 q^{p_1} + K_2 \frac{dq^{p_2}}{dt} \tag{3.21}$$

ここに、$K, K_1, K_2, p, p_1, p_2$は各モデルの定数です。

実測資料から$S \sim q$関係を求めると、一般に流量の上昇期と下降期でループを描き二価関数となります。これを一価関数として取り扱うのが木村の貯留関数法です。Prasadは$S \sim q$関係の2価性を$dq/dt$の項を導入することによって表現していますが、星・山岡は式（3.20）の$K_2$が$q$に依存しないようにするために$p_2$なるパラメータを導入して式（3.21）の式形を提案しました。

木村の貯留関数法は、遅滞時間の概念を導入して$S \sim q$関係に一価関数を適用できるようにしたもので、流出現象の非線形性をも簡便に表現できることから、わが国では最も実用に供されている洪水流出解析法の一つです。この方法の適用に当っては連続式と貯留関数を次のように書き改めます。

$$f \cdot r - (q - q_0)_l = \frac{dS_l}{dt} \tag{3.22}$$

$$S_l = K(q - q_0)_l^p \tag{3.23}$$

ここに、$r$は観測降雨強度、$f$は流入係数と呼ばれ流出率に近い性質をもちます。$q$は流出高、$q_0$は立上がり時の初期流出高、$(q - q_0)_l$は$(q - q_0)$の波形を$\tau$だけ左へ平行移動させた波形（図-3.4）、$\tau$は遅滞時間、式（3.23）が正の領域で一価関数になるように定められるもの、$S_l$は$fr$と$(q - q_0)_l$とによる見かけの流域貯留高、$K, p$：定数です。

図-3.4：貯留関数法による解析

$K, p$を実測資料から定めるには最適化手法による方法などもありますが、$S$が$q$の一価関数であることを利用する手法は次の手順によります。

1. $T_l$を仮定する。最初は$T_l = 0$とする。

2. 波形$(q - q_0)_l$をつくる。

3. $(q - q_0)_l$の増水期、減水期で同じ流出高$q_c$を与える時刻$t_1, t_2$を求める。$q_0$はピーク流出高の1〜2割とする。

4. 以下の関係から$f$を求める。

   $\int_{t_1}^{t_2} r dt - \int_{t_1}^{t_2} (q - q_0)_l dt = S_l(t_2) - S_l(t_1) = 0$

   $f = \int_{t_1}^{t_2} (q - q_0)_l \bigg/ \int_{t_1}^{t_1} r dt$

5. 求められた$f$を用いて、次式より$S_l(t)$を算出する。

   $S_l(t) - S_l(t_1) = \int_{t_1}^{t} fr dt - \int_{t_1}^{t} (q - q_0)_l dt$

   ここに、$S_l(t_1) = 0$とする。

6. $S_l(t)$と$(q - q_0)_l$の関係をグラフに描いて一価関数とみなせれば、その関数を$S_l = K(q - q_0)_l^p$の形として、$K, p$を定める。もし、ループを描けば$T_l$を変え①にもどる。このとき、$(q - q_0)_l$を横軸、$S_l$を縦軸として時計まわりのループなら$T_l$を大きく、反時計まわりなら小さくする。こうして、ループが小さくなるまで①〜⑥を繰り返す。

定数決定の手順中で、流入係数$f$は一定としていますが、実際の流出計算にあたっては有効降雨強度$r_e$を観測降雨強度$r$に対して次のように考える場合が多いです。

$$\begin{cases} r_e = f_1 r, & 0 < R < R_{sa} \\ \quad = f_2 r, & R_{sa} \leq R \end{cases} \tag{3.24}$$

これは面積$A$の流域が、面積$f_1 A$（$f_1$：一次流出率）の流出域と、面積$（1-f_1）A$の浸透域に分けられ、流出域からは100%流出し、浸透域では累加雨量$R$が飽和雨量$R_{sa}$に達してから流出が始まるという考え方です。飽和流出率$f_2$は通常1とし、$f_1$と$R_{sa}$の値は第四紀火山岩流域と非第四紀火山岩流域の区分のもとに与えられています。

定数決定後の流出計算には、図解法問と数値計算法が用意されています。わが国の十数の山地河川流域について$S \sim q$関係を調べることにより、$K, p$および$T_l$の総合化が図られ、次式が提案されています。

$$S_l = 40.3 q_l^{0.5} \tag{3.25}$$

$$\begin{cases} T_l = 0.047 L - 0.56, & L > 11.9 \text{ km} \\ \quad = 0, & L \leq 11.9 \text{ km} \end{cases} \tag{3.26}$$

ここに、$L$は流出地点から流路沿い流域内最遠点までの距離です。

式（3.25）は、総合貯留関数と呼ばれ、流量資料のない流域での流出量の推算に用いられますが、あくまで目安を与えるものである点に注意を要します。

分布定数系である後述のkinematic waveモデルを集中化することによって、$S \sim q$関係を求め、その物理的意義を明らかにする研究、さらにkinematic waveパラメータと流域特性値を用いて貯留関数パラメータを総合化する試みがなされています。

タンクモデル

タンクモデルは、図3.5に示すように、通常1〜2個の横孔と1つの底孔をもつタンクをいく段か重ね、横孔は流出、底孔は浸透になぞらえて、流域からの流出を表現するモデルです。流出高、浸透高とも孔より上の貯留高に比例するものと約束されています。タンクモデルは長期流出解析により威力を発揮します（3.5.1参照）が、洪水流出では通常直列2段ないし3段の構造が用いられます。

単位図法、貯留関数法、kinematic wave法などの洪水流出モデルが有効降雨の評価を必要とするのに対して、タンクモデルでは図-3.5で明らかなように損失機構を内蔵しているのが特徴です。

図-3.5：タンクモデルの説明図

長期流出

タンクモデル

長期流出を対象とする場合は、地下水流出、浸透、蒸発散、あるいは積雪地域では融雪といった要素を考慮しなければなりません。水資源問題などを考えるときには、洪水流出成分も評価する必要があります。これらを図3.5の型のタンクの組合せにより、雨水の損失機構、保留・浸透機構を内蔵し、流出の非線形性を巧みに表現したのが菅原のタンクモデルです。わが国の河川では通常図-3.6に示すような直列4段モデルが使用され、1段目タンクは表面流出、2段目は中間流出、3段目は準基底流出、4段目は基底流出に対応するとされています。

菅原がわが国の約30河川に対して、日流出高（mm/日）を解析した手順と結果は次のようです。

1. 各パラメータは図-3.6に示す範囲にあるものが多いです。ただし、$\lambda$($l$/日)はタンク底からの水深が$h$のとき流出強度を$q=\lambda(h-h_0)$と表わす流出孔係数、$h_0$はタンク底からの孔の高さです。
2. 洪水流出を表わす上段タンクにおいて、特に流出孔の位置と係数値が河川ごとに異なり、流域特性の違いが現れています。
3. 計算は入力としての雨を日雨量（mm/日）として、最上段のタンクに入れますが、無降雨日にはパン蒸発計の日蒸発量（mm/日）の7〜8割程度の値を最上段タンクから差し引きます。最上段が空になると、2段目タンクから差し引きます。以下同様に順次下のタンクから差し引いていきます。
4. 積雪・融雪の評価のためには、流域を標高によって地帯区分します。各地帯の代表気温に応じて、降水が雨か雪かを判断するとともに、融雪量も算定します。

タンクモデルでは、パラメータを試行錯誤的に決めなければならないのが難点ともいわれますが、パラメータを自動的に定める方法も開発されています。流域をいくつかに分割し集中面積の概念を利用すると、わが国では、どの流域とも流出孔係数を一定と考えてよいという研究もあります。

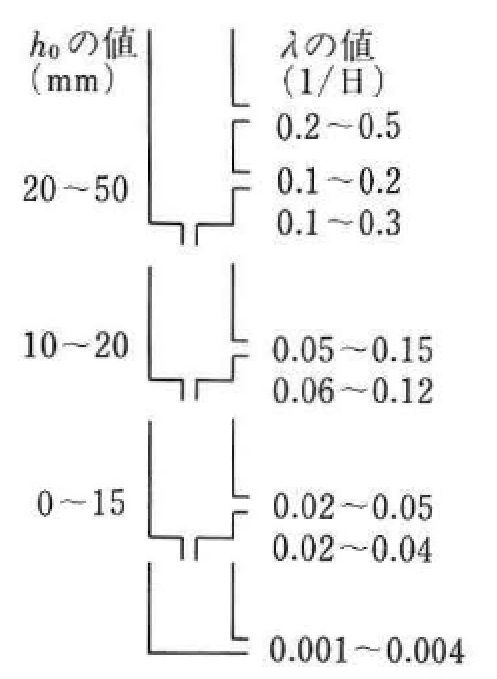
図-3.6：洪水用タンクモデルの定数の例

応答型モデル

長期流出に線形応答型のモデルを適用しようとする場合、特に短期流出成分に非線形性が強く現れるために、あらかじめその非線形成分を取り除くか、適当な非線形変換を施しておかなければなりません。

高梗らは、前者の立場をとり、表面流出成分となる降雨分と蒸発散に費される降雨分を差し引いた残りの降雨は、中間流出と地下水流出に対応し、その変換系を線形であるとの考えのもとに、いわゆる単位図法の適用を図っています。具体的には、長期流出成分（中間流出と地下水流出）に対する有効雨量の分離にあたって、降雨期と融雪期に分けます。降雨期では表層（A層）の保水特性を考慮して有効降雨を分離し、融雪期には気温と降雨に基づく積雪・融雪流出量から有効降雨の算定を行っています。全流出量から表面流出分を分離した流出量時系列と前記のようにして求めた有効降雨時系列の間にWiener・Hopf方程式を適用して得られた核を「統計的単位図」と呼んでいます。

日野は日降水量時系列と流量時系列の各々をべき乗変換した後、高棒らと同様なWienerの炉波・予測理論の適用を試みています。

また、式（3.10）を非線形応答系に拡張したボルテラ型積分級数の適用の試みもあります。ボルテラ型積分級数は

$$q(t) = \int_0^\infty r_e(t - \tau) h_1(\tau)d\tau + \int_0^\infty \int_0^\infty r_e(t - \tau_1) r_e(t-\tau_2)h_2(\tau_1,\tau_2) d\tau_1 d\tau_2 + \cdots \tag{3.28}$$

ここに、$h_i(\tau_1, \tau_2, \ldots, \tau_i)$は$r_e(t)$の$i$次の作用を表わす応答関数（あるいは核）です。工学における応用としてはWienerによって非線形の雑音解析に用いられて以来、核の同定法に関する多くの手法が提案されています。流出解析の分野では式（3.28）の第2項まで、すなわち2次の非線形核まで考える場合が多いです。非線形核の推定法には、①重回帰式による手法、②核の直交関数展開法、および③フィルタ相関法が代表的手法です。①と②は、主として未知数が多くなる欠点を緩和しようとするもので、③は降雨時系列が白色雑音で近似できる場合に用いられます。

不飽和帯の特性、流れの機構を考慮したモデル

角屋らは、「補給能モデル」と呼ばれる山地河川の低水流出解析法を提案しています。モデルの基本的な考え方は、Hortonの浸透能の概念を地下水への補給能の概念に置き換え、それを地下水流出の解析に関連づけたものです。地下水流出量と地下水貯留量の間には、一次比例の関係をおいています。

$$Q = f_G [1 - e^{-c(t-t_0)}] + Q_0 e^{-ct} \tag{3.29}$$

$$f = f_c + (f_0 - f_c)e^{-bt} \tag{3.30}$$

$$f_G = \begin{cases} 0 & : t \leq t_0 \quad (w < w_c) \\ f_c A & : t_0 \leq t \leq t_1 \quad (w \geq w_c) \end{cases} \tag{3.31}$$

$$f_0 = \begin{cases} \frac{f_u - f_c}{W(w_s - w_h)} (E_p + f_c)t + f_e & : w < w_c \\ f_u - (f_u - f_*)e^{-kT} & : w \geq w_c \\ \end{cases} \\ k = \frac{E_p}{V_E}, \quad V_E = W(w_e - w_h)\tag{3.32}$$

ここに、$Q$は地下水流出流量、$Q_0$は降雨開始時刻の地下水流出流量、$c$は地下水流出の低減係数、$A$は流域面積、$f$は降雨期間中の補給能（浸透能）、$f_0$は初期補給能、$f_c$は最終補給能、$b=(f_u-f_c)/W(w_s-w_h)$、$w$は表層土含水比、$w_s$は飽和含水比、$w_h$は吸着係数、$w_c$は毛管飽和含水比、$f_u$は上限補給能、$f_e$は降雨終了時刻の補給能、$f_*$は$w=w_c$のときの補給能、$t$は式（3.29）および式（3.30）では降雨開始時刻よりの時間、式（3.32）では降雨終了時刻よりの時間、$T$は降雨終了後$w=w_c$（$f=f_*$)を原点とする時間、$t_0$は降雨開始後$w=w_c$になる時刻、$t_f$は降雨が終了して$w=w_c$になる時刻、$E_p$は蒸発散能、$W$は蒸発、補給能に関与する表層土の単位面積柱体重量です。

まず、式（3.29）は、地下水流出流量関係を示したもので、右辺第1項は降雨による増分、第2項はそれ以前の降雨補給による地下水流出流量を意味します。式（3.30）は、いわゆるHortonの浸透能の式であって、これを降雨期間中の補給能としています。式（3.32）は、降雨終了後の補給能の回復曲線です。これら3つの関係式が補給能モデルの基本ですが、それに含まれる各定数は、実測のハイドログラフと降雨記録を用いて求められます。