ヒストグラム

ヒストグラムの概要

ヒストグラムは、データの分布状態を知るために多く用いられる統計的手法である。横軸に品質特性値（データ）の存在する範囲をいくつかの区間に分け、それぞれの区間に入るデータの数を度数として縦軸にとった図である。図が柱状になっていることから、柱状図（度数分布図）とも呼ばれる。

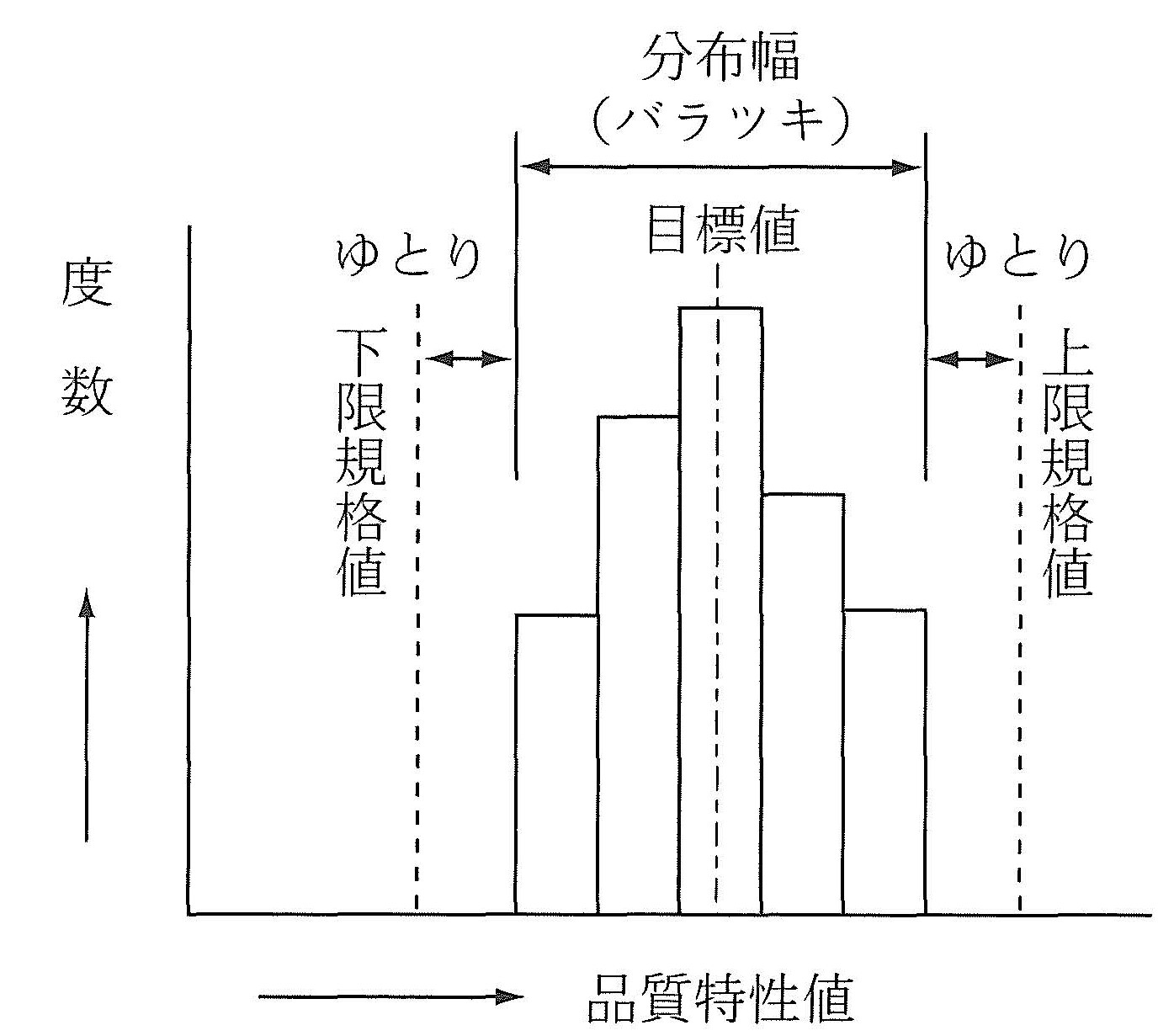
図-7：ヒストグラム

通常、ヒストグラムの中に品質管理の基準となる品質特性値の規格値を記入し、ヒストグラムの分布の平均値と中心値（目標値）および規格値を比較するなどして、規則性、工程の状態を把握することができる。ただし、ヒストグラムでは、個々のデータの時間的変化や変動の様子はわからない。ヒストグラムからわかることは、次のとおりである。

1. 分布の形状
2. 分布の中心位置（平均値）と中心値（目標値）との関係
3. 分布の広がり
4. 飛び離れたデータの有無
5. 規格値との関係

ヒストグラムの作り方

ヒストグラムを作る一般的手順は、以下のとおりである。また、同時にヒストグラムの作り方の例を示す。

手順１. 最近のデータをできるだけ多く集める。

列	1 列	2 列	3 列	4 列	5 列
1	22	22	23	23	24
2	24	23	23	23	22
3	22	22	22	23	23
4	22	23	22	21	25
5	23	23	22	25	23
6	23	21	24	19	21
7	23	23	22	23	21
8	21	23	22	21	24
9	25	24	27	23

手順２. データの中から最大値$X_{max}$、最小値$X_{max}$を求める。

ここでは、最大値$X_{max} = 27$、最小値$X_{max} = 19$　となる。

列	1 列	2 列	3 列	4 列	5 列
$X_{max}$	25	24	27	25	25
$X_{min}$	21	21	22	19	21

手順３. 全体の範囲、$R = X_{max} - X_{min}$を求める。

ここでは、範囲 $R = 27 - 19 = 8$

手順４. クラス分けする時のクラス幅を決める。

建設工事の場合、データの数が少ないときは、クラスの数を $5$ ~ $8$ としてかまわない。

$R$ ÷（クラスの数）= $C'$

$C'$を測定値の位に合わせ、これをクラスの幅$C$とする。

データの数	クラスの数
50 以下	5~8
100 以内	10
500 程度	10~15
1,000 以上	20

手順５. $X_{max}$、$X_{min}$を含むようにクラスの幅$C$で区切り、各クラスを設ける。

このとき、クラスの境界に位置するデータは、測定単位より一桁下の 5 単位で区切るとよい。これは、データを分ける場合に、はっきりどのクラスに属するかを決めるためである。

手順６. クラスの中心値（代表値）を求める。

手順７. データを各クラスに分けて度数分布表を作る。

このときチェックマークには////を用い、"正"は用いない。なお、このチェックは単純作業で間違いやすいので、2 度行う必要がある。

手順８. 横軸に品質特性値、縦軸に度数をとって、ヒストグラムを作る。

手順９. ヒストグラムに、規格値（上限または下限）を記入する。

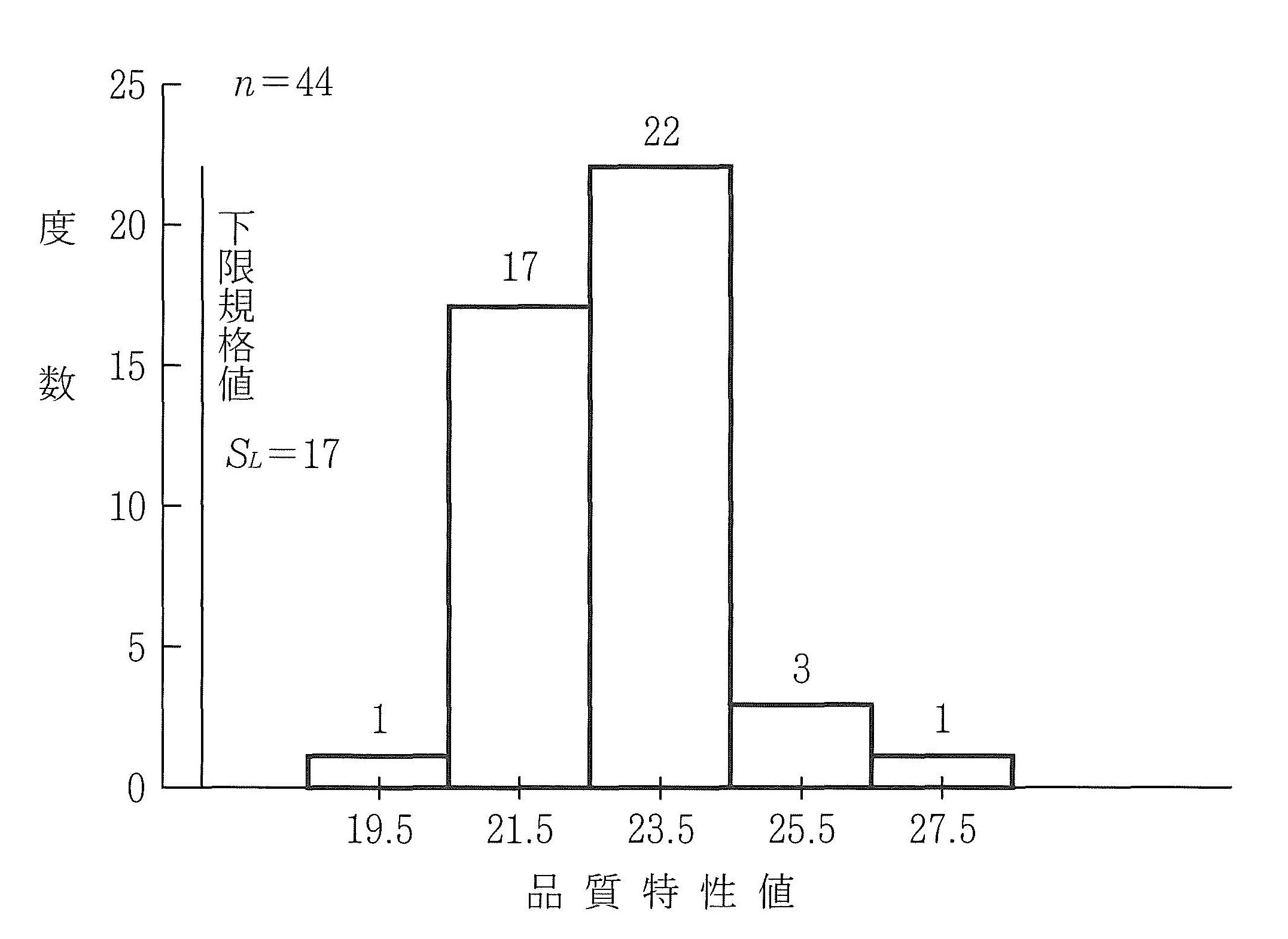
図-8：ヒストグラム完成例

ヒストグラムの見方

分布形状および規格との比較

測定値のヒストグラムは、一般に、中心付近が最も高く、中心から離れるほど低くなる左右対称のつり鐘型を示すことが多いが、実際には、種々の要因によっていろいろな形状のものが生まれる。

規格や目標値が決まっている場合には、ヒストグラムに規格値（上限、下限）、目標値を線で記入し、ヒストグラムが規格値に対して十分なゆとりをもっておさまっているかどうかを見る。

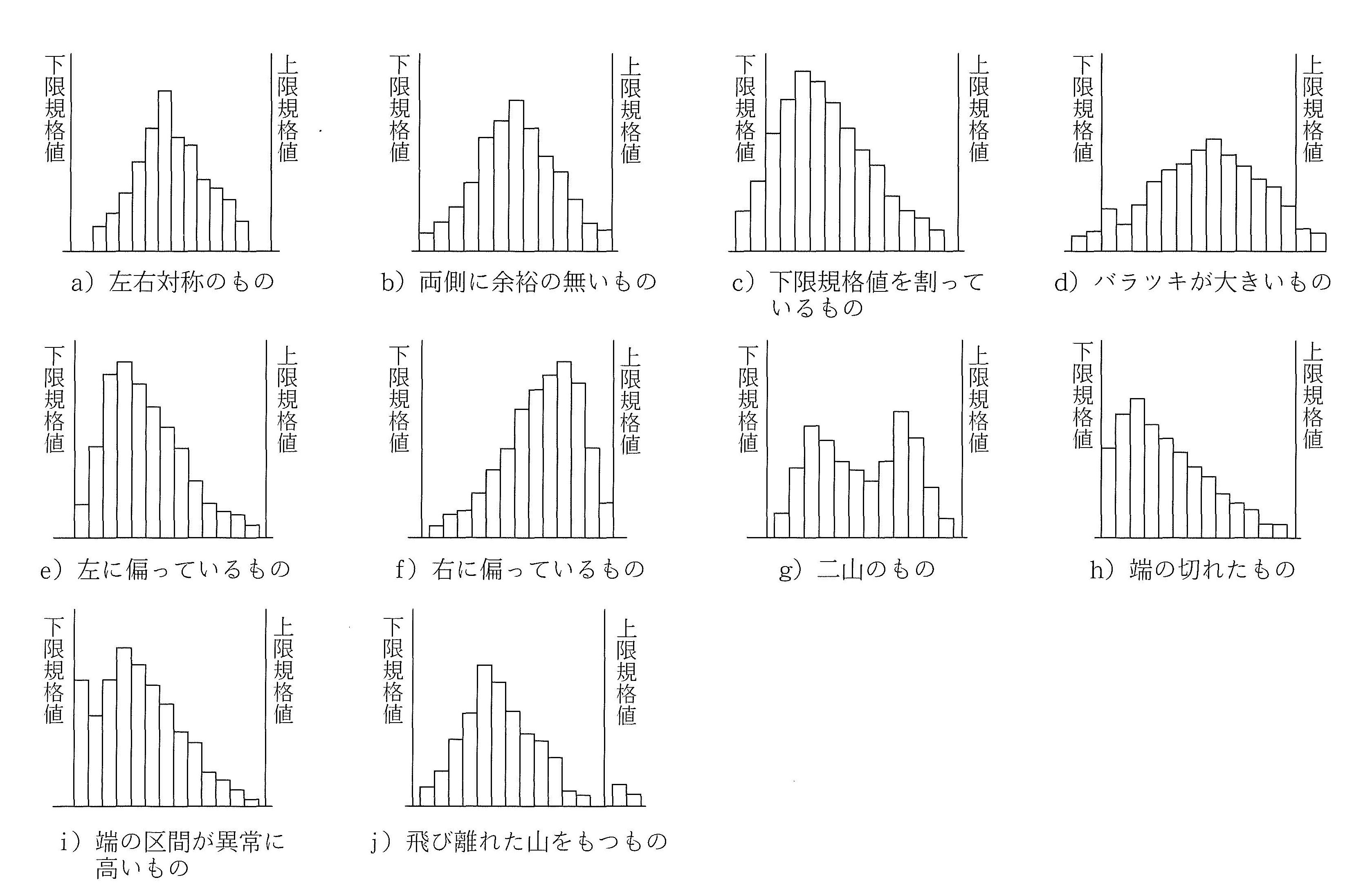
図-9：ヒストグラムの分布形状

これらのヒストグラムの形状と品質管理あるいは工程管理との一般的な関係は、以下のとおりである。

• a）規格値に対するバラツキもよくゆとりもあり、平均値も規格値の中心と一致する。品質管理上の理想的な型。
• b）規格値の範囲内であるが、わずかな工程の変化によって規格値を割るものがでるので、バラツキをもっと小さくするよう品質管理する必要がある。
• c）分布全体が左に寄りすぎ、下限の規格値を割っている。平均値を大きい方にずらし、バラツキを小さくするよう処置する必要がある。
• d）上・下限の規格値をともに割っており、応急措置が必要である。バラツキを小さくするための要因(現状の技術レベルまたは作業標準)を解析し、根本的な対策を採ることが必要である。
• e,f）上限または下限が規格値などで抑えられた場合で、特定の値以下または以上の値をとることが許されない場合によく現れる形状である。
• g）1 つの製品の製作に 2 つの異なる工程(2 台の機械や 2 種類の原材料)を用いた場合に現れやすい分布であり、平均値の異なる 2 つの分布が混在している。
• h）規格値以下のものを工程の途中で全数取り除いた場合に現れる。
• i）規格値以下のものを手直ししたり、データを偽って報告した場合に現れる。
• j）測定に誤りがあったり、工程に時折異常があった場合に現れる。

留意点

ヒストグラムを見る場合は、以下の点に留意する必要がある。

1. 規格値を満足しているかどうか。
2. 分布の位置は適当か。
3. 分布の幅はどうか。
4. 離れ島のように飛び離れたデータはないか。
5. 分布の右か左かが、絶壁型となっていないか。
6. 分布の山が 2 つ以上ないか。

なお、ヒストグラムにより品質管理の判定を行う際には、規格値に対するゆとりがどの程度あるかを統計手法により計算して確認しておくことが望ましい。

品質管理においては、このようにしてヒストグラムを見ながら、品質全体の傾向や規則性をつかみ、不良原因や問題点を追求するとともに、速やかに改善などの是正措置をとる必要がある。このような品質管理を積み重ねることによって、技術上の新しい課題やその改善方法が見出され、施工技術が向上していくことになる。

統計量の計算

ヒストグラムを見ただけでは、分布の幅や中心位置はその概略値しかわからない。また、いくつかのヒストグラムを比較する場合は、各ヒストグラムの分布の差を正確に表現することが難しい。

このため、分布の姿としての性質を数量的に表すことができれば、だれもが一致した数値で比較判断することができて便利である。そこで、以下に示すような、各種の統計量が用いられている。

データの中心位置の表し方

平均値

測定値の算術平均。

例えば、測定値が $3,4,6,7,10$のとき、$\bar{X} =(3+4+6+7+10) ÷ 5 = 6$

メディアン（中央値）

測定値を大きさの順に並べたとき、ちょうど中央にあたる 1 つの値（奇数個の場合）、または中央の 2 つの値の算術平均（偶数個の場合）。

測定値が $3,4,6,7,10$のときは、$X=6$。

また、測定値が $4,6,7,10$のときは、$X=(6+7)÷ 2 = 6.5$。

データのばらつきの表し方

範囲（$R$:レンジ）

測定値の最大値と最小値の差。

上の例では、$R = 10 - 3 = 7$

平方和（$S$:残差平方和）

個々のデータの平均値と各データとの差を二乗したものの和。

上の例では、$S=(10-6)^2+(7-6)^2+(6-6)^2+(4-6)^2+(3-6)^2 = 30$

分散($s^2$)

バラツキの程度を見るためには、残差平方和では不便であり、データ個別あたりのバラツキの程度を求める必要がある。これを分散という。

上の例では、$s^2 = 30 ÷ 5 = 6$

不偏分散（$V$）

残差平方和 S を（$n-1$）で割ったもの。

上の例では、$V = 30 ÷ (5-1) = 7.5$

標準偏差（$s$または$σ$）

不偏分散の正の平方根を標準偏差といい、データのバラツキを知るために最もよく用いられる。

上の例では、$σ = \sqrt{V} = \sqrt{7.5} = 2.74$

規格値に対するゆとりの計算

分布が余裕をもって規格値を満足しているかどうかは、ヒストグラムによって調べられる。この場合、まず平均値 X が規格値を満足していることを確かめたのち、次に示す方法によって、分布がゆとりをもって規格値を満足しているかどうかを数値計算して、チェックする。

片側に規格値がある場合は、

$$\frac{|S*{u}(*{or} S\_{L})-\bar{X}|}{σ} ≧ 3$$

ここで、$S_{u}$は上限規格値、$S_{t}$は下限規格値で、上式は上・下限規格値から平均値$\bar{X}$を引いた絶対値を標準偏差$σ$で割ったものが 3~4 あれば、ゆとりがあるということである。

すなわち、規格値よりプラス・マイナス標準偏差の 3~4 倍以内に平均値があれば、ゆとりがあることになる。