画像・レーザー計測

概説

三次元形状は、景観シミュレーションやハザードマップなどでの利用をはじめ、基盤的な情報として重要なものです。

一般的に、三次元形状の計測には写真測量が適用されてきました。

写真測量による三次元計測

写真測量は、画像を応用して被写体に関する情報を得る技術です。わが国の地形図も、昭和初期から写真測量により作成されてきました。特に、人間の近付きがたい場所でも観測でき、高い効率性を持つという特徴を有します。

画像は、地形図での表現である正射投影と異なり、中心投影に基づくものです。中心投影においては、高さ、あるいは奥行の差が画像上では平面的なずれとして表されます。これを基に、三次元計測が可能となります。

複数枚の画像から同一点を画像上で計測すれば、画像面上でのずれである視差が観測されます。これらの画像を立体視することにより、対象点の三次元座標を特定することが可能になります。このためには、カメラの位置と傾きがわかっていなくてはなりません。

撮影ごとに求めることになるカメラの位置と傾きを外部標定要素といいます。これに対し、カメラの画面距離や主点位置のずれ、レンズひずみなど、カメラ固有のパラメーターを内部標定要素といいます。これらの標定要素を求めることを標定と呼びます。

1枚の画像に対する単写真標定のためには、画像と地上の座標間の幾何学的関係である共線条件に基づき、後方交会法を適用します。これらの基本的原理は動画像にも適用することが可能です。画像計測については次項で説明します。

参考リンク

• 国土地理院 - オルソ画像について

レーザー計測による三次元計測

近年では、レーザー光を発射し、その反射波を計測することにより直接的に三次元計測を行う手法も広く利用されています。レーザーは、誘導放射による光の増幅の一般名称です。増幅されたレーザーは、単一波長であり、位相が一致し、方向も一致するという特徴を有します。

これらの特徴を利用し、発射波と反射波の時間差あるいは位相差を計測することにより、センサーから対象物までの距離を計測します。フェイズシフト方式では、変調した複数のレーザー光の位相差から距離を計測します。

専門的に用いられるものは、レーザー光を走査することにより面的に三次元計測を行うレーザースキャナーが通常です。一般的に用いられる1点までの距離を計測するレーザー距離計では、フェイズシフト方式のものが多いです。

レーザー計測の詳細については別項で紹介します。

参考リンク

• レーザースキャナーの原理

画像計測の原理

写真測量による三次元計測は、中心投影に基づく画像の平面的なずれを利用して行われます。

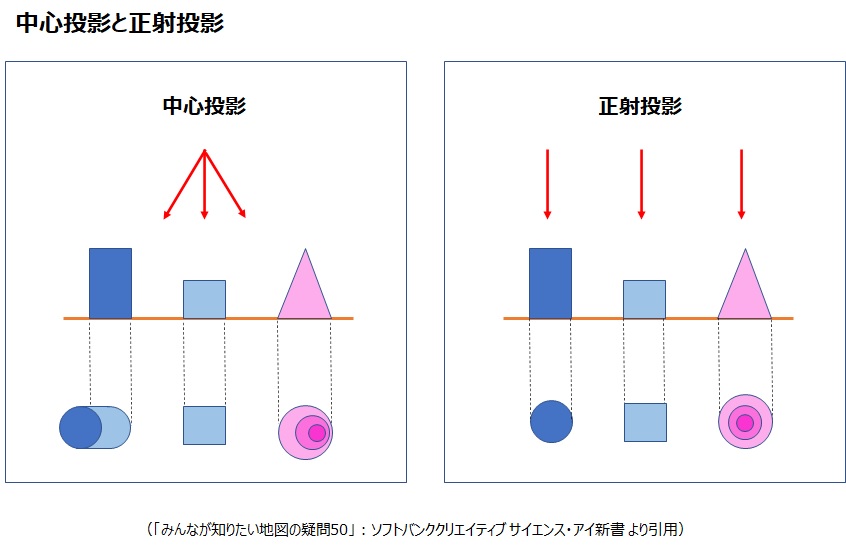
中心投影と正射投影の違い

地図などで用いられる正射投影は、光線を平行に投影するものです。一方、画像で用いられる中心投影は、光線がレンズの中心で集まるように投影されるものです。

中心投影では、地物の高さや奥行の差が、画像上で平面的なずれとして表されます。この平面的なずれを利用することで、三次元計測が可能となります。

立体視による三次元計測

複数の画像から同一の地物を観測した場合、画像間で平面的なずれ（視差）が生じます。この視差を利用して、立体視により三次元計測を行うことができます。

立体視では、同一の地物を異なる位置から撮影した複数の画像を用います。これらの画像から、地物上の同一点を特定し、その点の画像上での位置のずれ（視差）を計測します。

視差は、カメラの位置と地物までの距離に応じて変化します。カメラの位置と姿勢（外部標定要素）、およびカメラの内部パラメータ（内部標定要素）が既知であれば、視差から地物上の点の三次元位置を計算することができます。

このように、写真測量では、中心投影に基づく画像の平面的なずれを利用し、立体視の原理に基づいて三次元計測を行います。

用語の定義

写真測量で用いられる主な用語について、以下のように定義します。

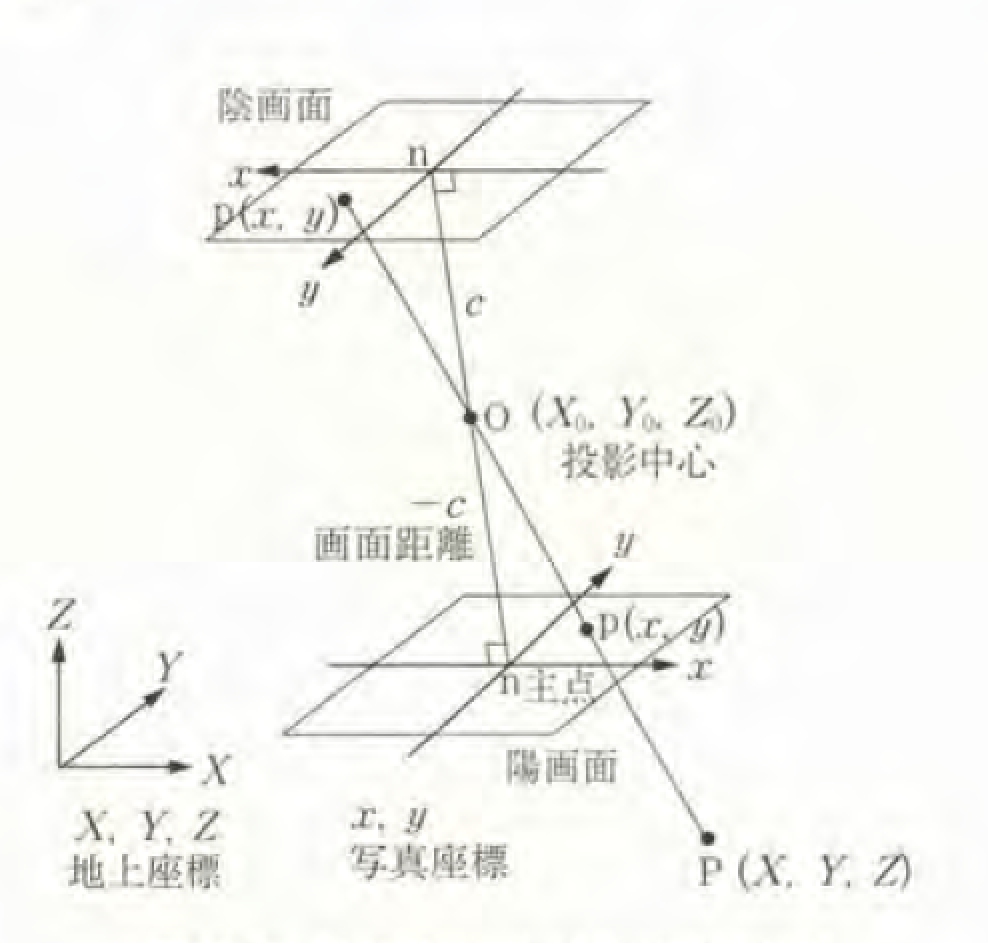
図-3：写真測量における用語の定義

• 投影中心O($X_0, Y_0, Z_0$): カメラの光学中心であり、光線が集まる点。
• 対象物P($X, Y, Z$): 撮影される対象物上の点。
• 陰画面: カメラの構造上、投影中心に対して対象物とは逆側に存在する画像面。
• 陽画面: 陰画面を投影中心に関して反転させた仮想的な画面。陽画面と陰画面は数学的に等価。
• 画像上の点p($x, y$): 対象物Pが画像上に投影された点。
• 主点n: 投影中心から画像面への垂線の足。
• 画面距離c: 投影中心と主点の距離。
• 地上座標: 三次元空間の座標系。
• 写真座標: 画像上の二次元座標系。

これらの用語を用いて、以降の説明を行います。

三次元計測の原理

人間が立体感を感じることができるのは、左右それぞれの眼に入る光線の角度が異なるためです。この角度差は、網膜に写される像の位置ずれ量として知覚され、立体感を得ることができます。眼を画像に代替すれば、画像平面上のずれを計測して、立体視に基づき、三次元計測が可能になります。

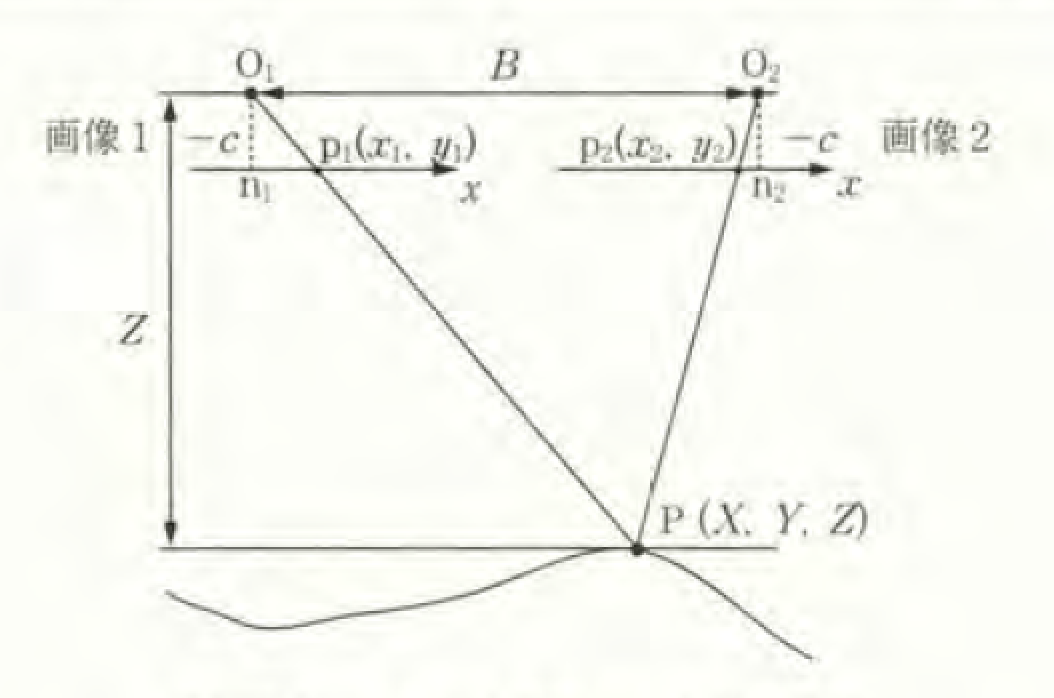
図-4：ステレオ画像による計測原理

いま、図-4のように2枚の画像が、画像間距離B（基線長）で平行撮影により得られたものとします。画面距離は共通でcです。両画像には、対象点Pが写され、それぞれ画像上で$p_1$、$p_2$として観測されたとします。画像1、2間の投影点の位置ずれ$x_1 - x_2 = p$を視差といいます。

幾何学的関係から、視差と三次元座標の関係は次のように表せます。

$$\frac{Z}{-c} = \frac{X}{x_1} = \frac{X-B}{x_2} = \frac{B}{x_1-x_2} = \frac{B}{p}, \qquad \frac{Z}{-c} = \frac{Y}{y_1} = \frac{Y}{y_2} \tag{15.15}$$

この式から、三次元座標を次のように導くことができます。

$$X = \frac{B}{p}x_1 = B + \frac{B}{p}x_2, \qquad Y = \frac{B}{p}y_1 = \frac{B}{p}y_2, \qquad Z = -\frac{cB}{p} \tag{15.16}$$

視差と三次元座標の計測精度の関係は次のように表すことができます。

$$\sigma_{XY} = \biggl(\frac{Z}{-c}\biggr)\sigma_p, \qquad \sigma_Z = \biggl(\frac{Z}{-c}\biggr)\biggl(\frac{Z}{B}\biggr)\sigma_p \tag{15.17}$$

ここで、$\sigma_{XY}$、$\sigma_Z$は、それぞれXY座標、Z座標の精度、$\sigma_p$は視差計測の精度です。高さや奥行といった$Z$座標の精度向上のためには、基線長$B$と対象物までの距離$Z$の比（基線高度比$B/Z$）を大きくすればよいことがわかります。

共線条件と単写真標定

上記の例では、平行撮影により得られた画像を用いていましたが、実際には、カメラは傾いて撮影されます。カメラの傾きがわかっていれば、平行撮影に変換可能であり、この変換を偏位修正といいます。さらに、三次元座標の計算において基線長を必要とすることから、カメラの位置も求めなくてはなりません。これらのカメラの位置と傾きを外部標定要素といいます。

一方、カメラの画面距離や主点位置のずれ、レンズひずみなど、カメラ固有のパラメーターを内部標定要素といいます。これらの標定要素を求めることが標定です。

ここでは、特に1枚の画像の標定要素を推定する単写真標定について解説します。なお、内部標定要素はキャリブレーションにより、対象物の撮影前に求めることができるため、内部標定要素は既知とし、外部標定要素のみを求めるものとします。

単写真標定のためには、写真座標と地上座標が満たすべき幾何学的関係である共線条件が重要になります。図-5に示すとおり、対象物$P_1$、$P_2$、$P_3$を撮影し、画像投影点$p_1$、$p_2$、$p_3$が観測されたとします。共線条件とは、光の直進性に基づいた、「点$P_1$、投影中心O、画像投影像$p_1$は、同一直線上にある」という条件です。

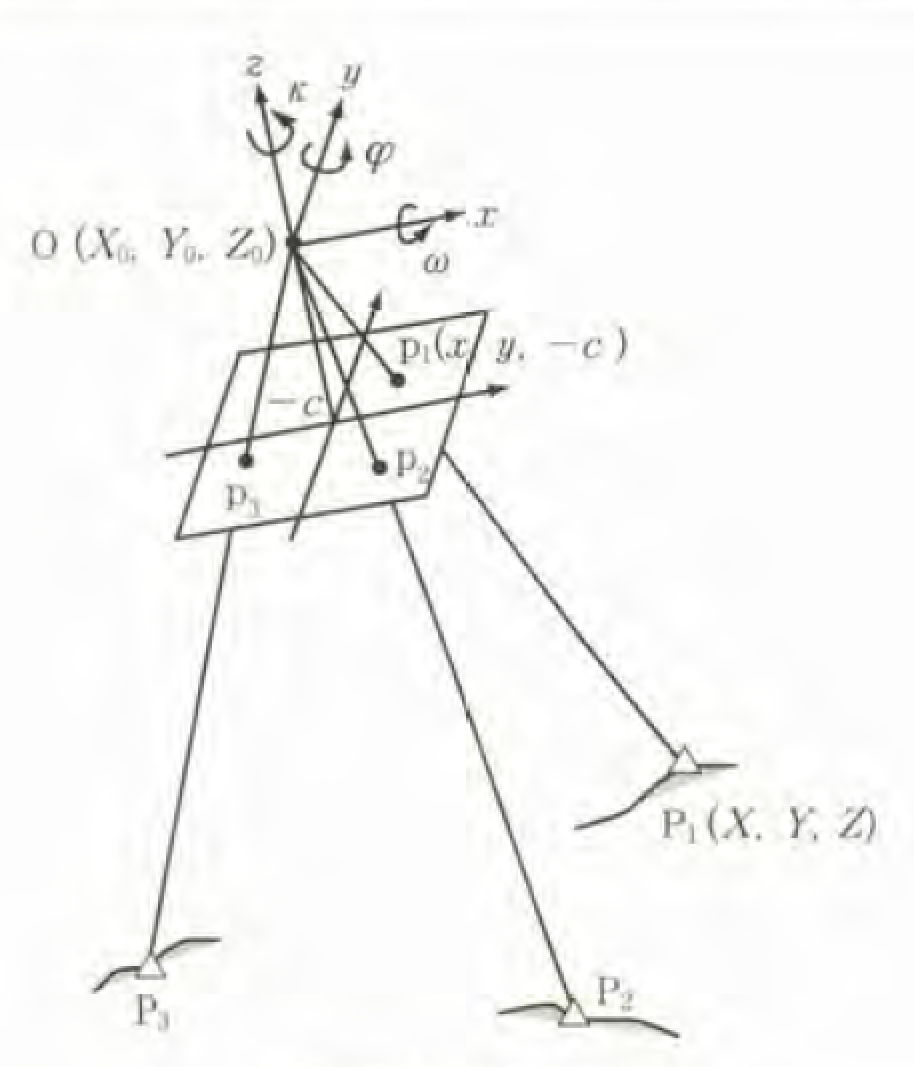
図-5：共線条件

写真座標が地上座標に対して図のとおりに傾いていたとすると、共線条件に従えば、写真座標と地上座標の関係は次のように表すことができます。

$$\begin{bmatrix} X - X_0 \\ Y - Y_0 \\ Z - Z_0 \end{bmatrix} = \frac{1}{m}D \begin{bmatrix} x \\ y \\ -c \end{bmatrix} \tag{15.18}$$

ここで、Dは対応する回転行列を示します。

$$D = \begin{bmatrix} l_1 & l_2 & l_3 \\ m_1 & m_2 & m_3 \\ n_1 & n_2 & n_3 \end{bmatrix} \tag{15.19}$$

式(15.15)を考慮すれば、式(15.18)より以下の共線条件式が導かれます。

$$\begin{aligned} x = -c\frac{l_1(X-X_0) + m_1(Y-Y_0) + n_1(Z-Z_0)}{l_3(X-X_0) + m_3(Y-Y_0) + n_3(Z-Z_0)} \\ \\ y = -c\frac{l_2(X-X_0) + m_2(Y-Y_0) + n_2(Z-Z_0)}{l_3(X-X_0) + m_3(Y-Y_0) + n_3(Z-Z_0)} \\ \end{aligned} \tag{15.20}$$

次に、共線条件式に基づき、外部標定要素であるカメラの位置($X_0, Y_0, Z_0$)と傾き($\omega, \varphi, \kappa$)を求めます。図中の対象物中の点$P_1$、$P_2$、$P_3$とその投影像$p_1$、$p_2$、$p_3$がつくる光線は、1点で交わらなければなりません。すなわち、すべての点が共線条件を満足するように外部標定要素を決定する後方交会法を適用します。

ここでは、写真座標と地上座標の両者とも既知である地上基準点を用います。未知パラメーターは六つの外部標定要素($X_0, Y_0, Z_0, \omega, \varphi, \kappa$)であり、一つの地上基準点当り二つの共線条件式が得られるため、少なくとも3点の地上基準点によって外部標定要素を決定することが可能です。通常は、誤差を伴うため、4点以上用いて最小二乗法により求めます。ただし、共線条件式は非線形であるため、非線形最小二乗法を適用します。そのため、単写真標定においては、初期値が必要となります。現在では、GNSSやIMU（慣性計測装置）などにより、初期値を取得することが可能です。

内部標定要素が未知の場合には、共線条件式において、写真座標($x, y$)を未知パラメーターである主点位置のずれとレンズひずみの近似値を考慮して補正し、画面距離$-c$を未知パラメーターとして扱えばよいです。

複数枚の画像に同時に共線条件式を適用するバンドル調整が用いられることも多いです。バンドル調整では、使用する全画像の外部標定要素に加え、座標未知点の三次元座標も未知パラメーターとします。初期値としての未知点の三次元座標を同点が写っている画像に再投影し、その写真座標と観測された写真座標の差（交会残差）を算出します。交会残差の二乗和を最小化することにより、未知パラメーターの推定を行い、各パラメーターの更新を行います。

共面条件と相互標定

共線条件は、写真座標と地上座標が満たすべき幾何学的関係でしたが、もう一つの重要な条件は、ある画像の写真座標ともう1枚の写真座標が満たすべき関係である共面条件です。共面条件とは、「ステレオ画像において、投影中心2点および共通の対象点の各画像への画像投影点2点（パスポイント）が同一平面上にある」という条件です。

この共面条件を一組みのステレオ画像に適用し、二つのカメラ間の相対的な外部標定要素を求めることを相互標定といいます。いま、一方の画像の写真座標を任意座標系（モデル座標系）として固定した場合、もう一方の画像の外部標定要素のうち、X方向の位置は交会条件とは無関係です。そこで、この値を例えば1に固定すると、未知パラメーターは五つの外部標定要素($Y_0, Z_0, \omega, \varphi, \kappa$)となります。

一つのパスポイント当り一つの共面条件式が得られるため、少なくとも5点のパスポイントによって、外部標定要素を決定することが可能です。通常は、誤差を伴うため、6点以上用いて最小二乗法により求めます。共面条件式も非線形であるため、非線形最小二乗法を適用します。

相互標定結果から立体視を適用すれば、対象物と相似な三次元モデルを作成することが可能です。実スケールの三次元座標を求めるためには、地上基準点を用いて地上座標に変換します。これを絶対標定と呼びます。

レーザー計測

近年では、レーザー光を発射し、その反射波を計測することにより直接的に三次元計測を行う手法も広く利用されています。レーザーは、誘導放射による光の増幅の一般名称です。計測用のレーザーでよく用いられる波長帯は0.7-1.3μmの近赤外領域です。

レーザー光の特徴と距離計測の原理

増幅されたレーザーは、単一波長であり、位相が一致し、方向も一致するという特徴を有します。この特徴を利用し、GNSSやIMUなどで位置と姿勢がわかっているレーザーセンサから、計測対象にレーザー光を発射し、反射した光を受光盤で捉えます。発射波と反射波の時間差や位相差を計測することにより、センサーから対象物までの距離を計測します。

位相差を計測するフェイズシフト方式では、変調した複数のレーザー光の位相差から距離を計測します。位相を計測する場合には、波数までは不明です。そのため、十分に周波数が低いレーザー光により概略距離を算出し、より高周波数のレーザー光により、距離測定の解像度を向上させます。

なお、後述する5mメッシュ標高データ作成に用いられている航空レーザーの多くは、計測点の高さは1cm単位で記録され、高さの精度は±15cm程度です。

空中からの画像計測においては、レーザーを用いても、直接得られる高さのデータは、建造物や植物の高さを含んだものです。このような地物の高さを含んだ標高モデルをDSMといいます。一方、地物の高さをフィルタリングにより除去し、地盤高を表現した標高モデルをDTMといいます。5mメッシュ標高データは、DTMの代表例です。

画像計測、レーザー以外にも、レーダーによる三次元計測も可能です。

デジタル標高地形図の作成

前項のレーザー計測技術により、詳細な地形データが作成されています。国土地理院が提供する5mメッシュ標高データ標高データは、航空レーザーにより取得されたデータから作成されたものです。現在では、基盤地図情報の一部として、無償でインターネットからダウンロード可能です。

参考リンク

• 基盤地図情報

オリジナルのレーザー計測データは、地物の高さも含んだものです。DTMである5mメッシュ標高データを作成するために、フィルタリング処理を行います。1本のレーザー光において、反射波の反射強度が強い部分を、離散的に複数記録することができます。この反射強度が強い部分に、物体、あるいは地盤が存在すると仮定します。

地上測量の成果なども参照し、この中から、地盤まで達していると推定される計測値のみを用います。また、平面をメッシュに区切り、そのメッシュ内の三次元形状を多項式により回帰します。計測点が推定された多項式から閾値以上離れていた場合には、地物として判定し、その点を除外します。フィルタリング後は、その結果を目視によっても点検しています。以上の処理で残った計測点を内挿補間することにより、メッシュ標高データを作成します。

従来公開されていた地形データのおもなものは、写真測量に基づき作成された1/25000地形図の等高線から発生させた50mメッシュ標高データでした。5mメッシュという空間解像度の大幅な向上により、微地形を読み解くことがより容易になりました。特に、都市域における地形表現力が格段に上がり、その利用価値も高いです。

例えば、ハザードマップへの利用など、自治体における利用も盛んです。また、詳細な地形解析への応用も見られます。近年の地形ブームにより、都市部の地形に関する多種の出版物が刊行されていますが、その中でもよく利用されています。

この5mメッシュ標高データを陰影段彩図として表現し、1/25000地形図を重ね合わせた地形図が、「1/25000デジタル標高地形図」です（図-6参照）。陰影段彩図とは、高い標高から低い標高までを暖色系から寒色系へと連続的な色で表現したものに、一定方向からの光を当てた場合の陰影を加えたものです。デジタル標高地形図は、現在では、東京都区部、名古屋、濃尾平野西部、大阪、福岡、高知などで作成されています。

例えば、低地における地形把握においては、デジタル標高地形図を用いれば、その微地形情報から、自然堤防などの地形を読むことができます。国土管理の上でも、必要不可欠な地形図となっています。

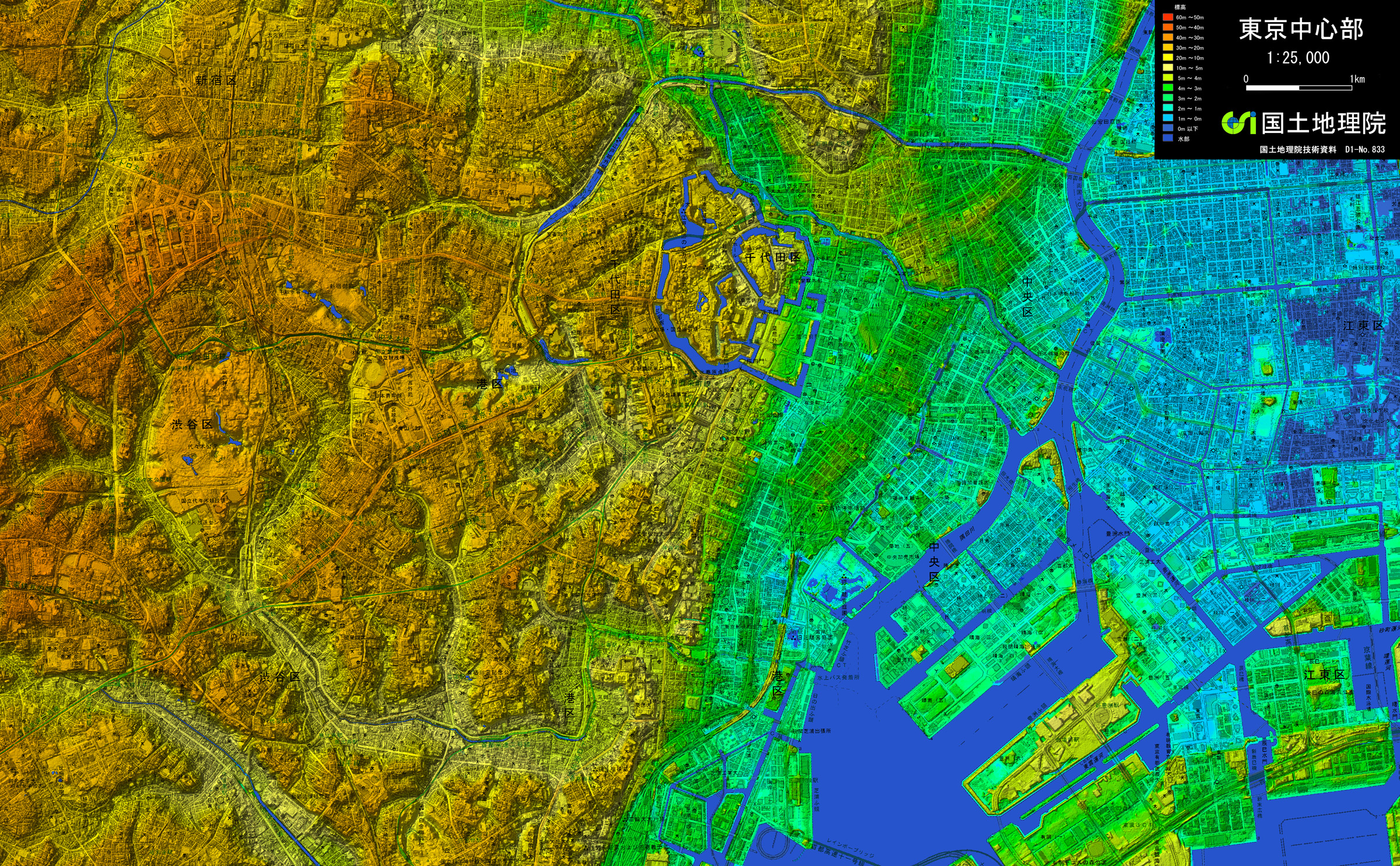
図-6：デジタル標高地形図（国土地理院）

移動体認識への応用

車両の実空間での位置計測

交通渋滞、交通事故、交通環境負荷等に対する詳細分析に向け、定点における個別車両の詳細な移動履歴データが必要とされています。この要請に応える手段として、空中からのビデオカメラによる観測が考えられます。この動画像に対して、画像処理手法による画像上での車両の認識、追跡手法も開発されています。

認識結果を交通現象分析などへ応用する際には、実空間座標での車両位置が必要となります。道路上のみを移動する車両の位置を求める問題として、単一ビデオカメラによる車両の実空間での位置計測を行います。

動画像中でステレオ画像の関係にあるフレームを選択し、標定および立体視の原理を適用することにより、静止物体である対象道路の三次元計測が可能となります。つぎに、動画像の全フレームにおける道路部を先のステレオ画像の一方に幾何補正します。画像上での車両位置は、すでに認識されているため、その写真座標から道路上の座標を求めることにより、実空間での車両位置の計測が達成されます。

三次元情報を用いた人物の認識と追跡

以上の例では、対象物の認識後に写真測量の原理に基づき、三次元計測を行うものでした。逆に、三次元計測結果は、対象物の認識に有用であると考えられます。つぎの例では、固定されたステレオビデオカメラにより、動画像と同時に得られる各画素に対応する点の三次元座標を用いて移動体を認識する例を示します。

ここでの対象は、人物の位置計測とします。人物挙動の詳細な把握は、公共空間などにおける設計などにも必要とされているものです。これまでも、ビデオカメラによる人物の動きの観測が行われてきました。しかしながら、動画像のみを用いた画像処理手法では、人物相互の遮蔽が存在する場合の認識精度の低下という課題がありました。ここに、三次元情報を利用すれば、個々人の抽出・追跡を実現できることが期待されます。そこで、色情報と三次元情報を組み合わせて人物認識・追跡を行います。

前述のとおり、ここでは、各画素の色情報と、その画素に対応する実空間の三次元座標を利用します。ステレオビデオカメラは固定されているため、標定は終了しており、ステレオ画像の立体視により、この三次元座標が得られます。これらの観測情報から人物位置（人物重心の三次元座標）を推定します。

図-7：人物の認識・追跡結果

以上のとおり、動画像に写真測量を適用し、認識・追跡アルゴリズムを併用することにより、交通分析の基礎情報となる、移動体の位置情報を取得することができ、効率的な調査への貢献が期待されます。