河川計画

計画規模

中小河川の計画規模は、基本的に降雨量の年超過確率で評価することとし、その設定に当っては、河川の重要度、既往洪水による被害の実態、経済性、上下流のバランス等を総合的に考慮して定める。

中小河川計画の手引き(案)p. 17

河川の計画規模は、一般に水文量の年超過確率で表される。中小河川の場合、雨量資料は水位・流量等に比べ蓄積度合いが高く、流域や河道の改変による人為的影響を受けないことに加え、大河川と比べると降雨の地域的な一様性が高く、雨量と流量の規模の相関が高いことなどの理由から、雨量を計画の外力として扱うのが合理的である。

以下に、計画規模の設定にあたっての基本方針を示す。

1. 計画規模の設定に当たっては、河川の大きさ、流域の社会経済的重要性、想定される被害の実態、過去の災害の履歴、経済効果に加え、上下流バランス、流域の将来の姿などに配慮する。

2. 河川の重要度を評価する流域の指標として、流域面積、流域の都市化状況、氾濫区域の面積、資産、人口、工業出荷額等が考えられるが、このほか水系として一貫した上下流、本支川でバランスが保たれ、また都道府県内の他河川とのバランスにも配慮して決定するものとする。

さらに、計画規模決定にあたっては、以下の点を総合的に考慮することが必要である。

• 県庁所在地をはじめとする県内の主要な都市を流れる河川である場合
• 過去に大規模な洪水被害を受けている場合
• 大規模開発が計画されている場合

これらの流域の状況を十分に考慮し、適切な計画規模を設定することが重要である。

高水計画

計画降雨

計画降雨の作成

計画降雨は流域の規模、降雨特性、計画対象施設の種類、さらには雨量資料の存在状況等を勘案して、適切に作成する。

中小河川計画の手引き(案)p. 35

基本高水を設定する方法としては、洪水の成因となる降雨を計画外力として、所定の計画規模に対応する計画降雨を定め、この計画降雨から流量に変換する方法を基本とする。

計画降雨は、降雨量、降雨量の時間分布及び地域分布の 3 要素で表されるが、その作成にあたっては流域の規模や降雨特性といった自然条件、洪水調節施設計画の有無といった検討目的を十分把握し、さらに雨量資料の存在状況等も勘案する必要がある。

降雨強度式

流域の規模等から降雨量の地域分布を無視しえると判断される場合は、降雨強度式を用いて計画降雨を作成する。

中小河川計画の手引き(案)p. 35

降雨強度式は、基本的に流域面積が 50km2 未満程度の合理式を用いる河川に適用されることが多いが、降雨量の時空間分布の検証を行い、降雨量の地域分布が無視しえる河川に適用することも可能である。

この場合、計画降雨の 3 要素のうち、降雨量（洪水到達時間内降雨強度）のみを考慮することとなる。なお、降雨強度式を適用するにあたり洪水到達時間をあらかじめ設定しておく必要がある。

中小河川の洪水到達時間内の短時間降雨強度式は、各都道府県で作成されたものを用いることとする。ただし、対象河川流域が短時間降雨強度式の作成に用いられた観測所と離れていたり、降雨特性が明らかに異なると考えられる場合には、近傍の気象庁アメダス観測所による確率短時間降雨強度式を用いることができる。

ヒント

• 兵庫県の降雨強度式

高水流量

高水流量決定の原則

河川整備基本方針で定める「基本高水のピーク流量·計画高水流量」(以下「高水流量」という)は、原則として、策定時点における最適手法により算定する。これによることが河川計画上著しく不合理となる場合には、個別に検討する。

中小河川計画の手引き(案)p. 74

工事実施基本計画·全体計画との整合

河川整備基本方針・河川整備計画策定時に、既に工事実施基本計画・全体計画で高水流量が定められ、事業を実施している場合には、新たに高水流量を設定するにあたり、下記のとおり留意する。

従前の計画に比べ高水流量が下がる場合

1. 既設構造物の評価
   • 既に完成した構造物は、現時点では余裕があるが、事業実施時点では適切な安全度であったと評価する。(原則として HWL は変更しない。ただし、これらによることが不合理な場合は適宜判断する。)
2. 今後の事業実施について
   • 今後の事業については新しい計画に基づいて実施するが、完成済み区間と隣接する場合等には、一連区間の河川計画の連続性を考慮して現場での対応を行う。

従前の計画に比べ高水流量が上がる場合

1. 既設構造物の評価
   • 既に完成した構造物は、事業実施時点では適切な安全度であったと評価するが、現時点では流下能力が不足することとなる。よって、再改修が必要となる。
2. 今後の事業実施について
   • 事業実施にあたっては、未改修区間と事業実施済み区間の優先度を判断する。未改修区間を先に実施する場合は、上下流バランスを考慮したうえで、手戻りのない計画で事業実施する。

従前の計画と高水が同じ場合

1. 既設構造物の評価
   • 既に完成した構造物は、現時点で評価しても、適切な安全度であると評価する。
2. 今後の事業実施について
   • 事業実施については、新しい計画に基づくものとして実施する。

流出解析

流出解析手法

降雨から流量への変換にあたっては、流域の規模および流量観測資料の有無や計画対象施設の種類、内水河川の扱い等の計画条件、将来の土地利用の変化や河道改修による流出特性の変化等考慮して適切な流出計算手法を採用する。

中小河川計画の手引き(案)p. 31

中小河川の流出計算手法としては、一般に以下の方法が用いられている。

合理式

合理式の特色は、流域の最遠点から考慮地点まで雨水が流下集中した時に最大流量が生じると考え、その時間を洪水到達時間と呼んでいることである。この方法は中小河川でよく用いられている。

合理式の長所は、ピーク流量算出にあたって最も簡便であり、適用例が多いことである。一方、短所としては、ハイドログラフを求めることができないので、ダム等の貯留施設の計画には用いることができない。また、実測値との検証についても困難である。さらに、流域面積が大きくなると適用が困難になる。

合理式の適用河川は、基本的に流量観測値がなく上流に洪水調節施設が存在しない河川とし、流域面積 50km2 未満程度が目安となる。

合成合理式

合成合理式は、基本的に洪水到達時間（tc）毎のハイエトグラフを作成し、tc 毎の合理式によるピーク流量を連ねてハイドログラフを作成するものである。

その長所は、簡易にハイドログラフが作成できることである。一方、短所としては、実測値との検証が困難であり、流域面積が大きくなると適用が困難になる。

合成合理式の適用河川は、合理式の適用が可能な河川でハイドログラフの算出が必要な場合に用いることができる。なお、合成合理式の考え方には、通常の合理式と同様に流量検討地点の上流を単流域として扱う方法と、流出モデルのように流域分割を行い河道の遅れ時間を考慮して合成ハイドログラフを算定する方法がある。

貯留関数法

貯留関数法は、貯留高と流出高との間に比較的簡易な式で非線形性を表現した手法で、日本のほとんどの一級河川で使用されている。この手法は、10 km2 から数 100km2 程度の流域で単流域として適用されており、土地利用の変化を考慮した方法も提案されている。

貯留関数法の長所は、特に山地が多くの割合を占める流域での適合度が良いことである。また、流域分割や流出系統作成の巧拙があまり問題にならない方法でもある。一級河川での適用例が多く、定数検証は主に$K$、$T1$の修正で済み、比較的容易である。

一方、短所としては、実用的ではあるものの、定数について水理学的裏付けが弱いことが挙げられる。小出水の際の定数を用いた場合、大出水の再現性に問題がある。また、一般に平地や都市域での適合度に劣る。

準線形貯留型モデル

合理式の到達時間内降雨強度の考え方を取り入れ、非線形性を表現した各地目毎の指数単位図である。この手法は、降雨流出の非線形性が扱え、流域の開発等の地目変更に伴う流出変化が扱えることから、開発が著しい流域で適用例が多くなっている。

合成単位図法の長所は、地目毎の流出計算結果を合成しているため、地目の改変や地目毎の貯留、浸透対策河川に適用性が高いことである。また、流域分割や流出系統の作成のしかたの巧拙は、特性曲線法ほど精度に影響しない。

一方、短所としては、計画論的に有効なモデルである反面、実績の再現性に難点がある場合があることが挙げられる。地目別定数 C についての総合化の程度に問題を残している。また、山地部のように貯留効果が大きいところでは、特に低減部再現性に難点がある。

特性曲線法(等価粗度法)

特性曲線法は、流域を幾つかの矩形斜面と流路が組み合わされたものと見なし、雨水流を水理学的に追跡した計算手法である。

この手法の長所は、流域の性状を等価粗度で表すところが特徴的で、流域開発の変化を反映させることができることである。比較的表面流が卓越する都市域について適合度が高くなる。

一方、短所としては、定数の構成要素が多く、かつそれぞれの要素を比較的高い精度で求める必要があり、手間がかかることが挙げられる。また、流域分割や流出系統作成のしかたの巧拙により精度が問題となる。

合理式の流出定数

合理式の洪水到達時間、流出係数については、流域及び河道の特性を踏まえて適切な値を採用するものとする。

中小河川計画の手引き(案)p. 57

洪水到達時間

一般に中小河川において適用し易い方法としては、次の３つが挙げられる。

1. クラーヘン（Kraven）式
2. 等流流速法
3. 土研式

このうち、クラーヘン式についてはその根拠が不明であるが、従来より慣用的に用いられている。

等流流速法はクラーヘン式の変形であり、洪水伝播速度を等流流速とするものである。

土研式は都市域と自然流域を対象に式が示されており、土地利用の変化に伴う洪水到達時間の変化を考慮でき、根拠が明らかであるため適用しやすいが、適用事例は少ない。土研式は流出試験地等の水文資料より、計画上の安全側を見込んで、洪水遅れ時間実測値の下限値を採用し、それを 2 倍して洪水到達時間としている。

クラーヘン式

クラーヘン式では、一般に雨水が流域から河道に至る流入時間と河道内の流下時間の和で示される。

流入時間

流入時間の設定については、以下のように整理されている。

• 山地流域：$2km^{2}$ $30$分
• 特に急傾斜面区域：$2km^{2}$ $20$分
• 下水道整備区域：$2km^{2}$ $30$分

基本的には、当該河川の流域から流入域$2km^{2}$を先取りし、上記の値を用いて流入時間を設定するとともに、流入域を除いた流域の河道延長を用いて河道流下時間を算定する（流入時間の最大値は上記値となる）。

ただし、流入域$2km^{2}$を除いた流域面積が極端に小さくなる場合には、地形図上で河道を示す青線の上流端の上流域を流入域とし、その流入時間を次のような方法で算定するとともに、青線の上流端から下流を河道として河道流下時間を算定する手法も用いられている。

参考

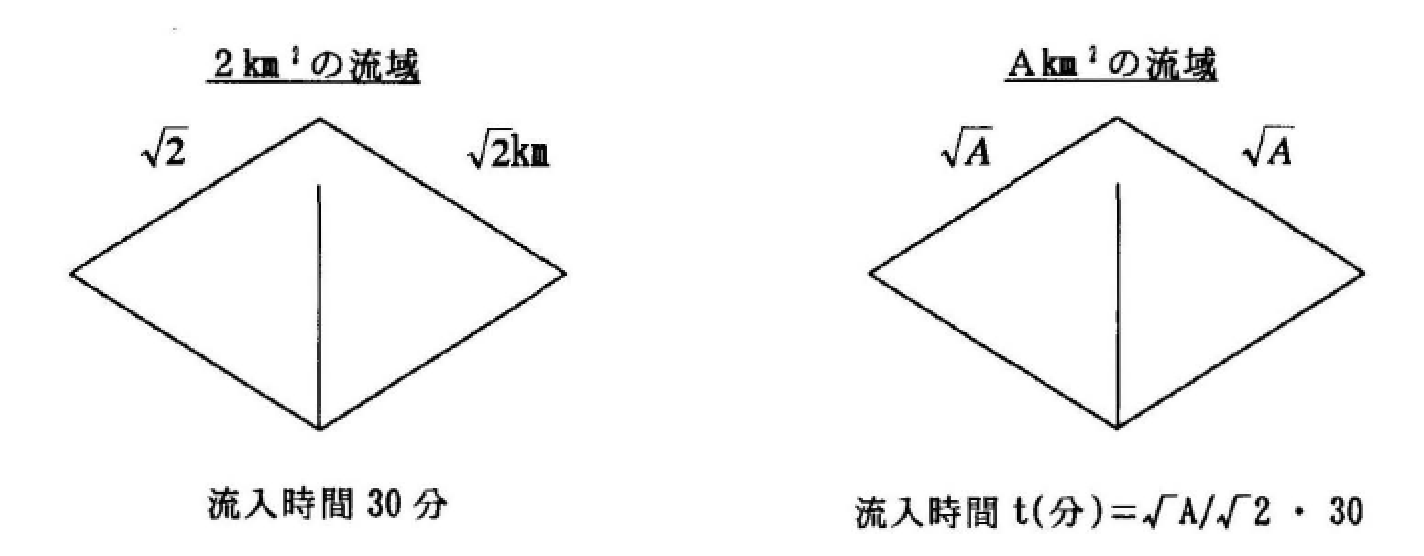
この他にルチーハ（Rziha）式、角屋式他種々の推定式が提案されている。 ルチーハ式は、わが国の河川に適用すると洪水到達時間が過大に算定される傾向にあると報告されている。 角屋式はその式中に到達時間内降雨強度を有し、未知数を含むこととなるのでトライアルの計算となり扱いが繁雑となる。

河道流下時間

河道流下時間$T$は次式で与えられる。

$${60} × \frac{L} {W}$$

ここに、

• $L$：河道上流端（流域から流入域 2km² を除いた流域の最遠点、又は$1/25,000$地形図で示されている水色の部分の最上流）から流量検討地点までの流路の距離（m）
• $W$：洪水伝播速度（m/s）

であり、クラーヘン式は洪水伝播速度として以下を与えている。

流路勾配$I$	1/100 以上	1/100 ～ 1/200	1/200 以下
洪水伝播速度$W$	3.5 m/s	3.0 m/s	2.1 m/s

ここで、$I$ : 河道上流端と懸案地点の標高差$H(m)$を流路長($L$)で割ったもの

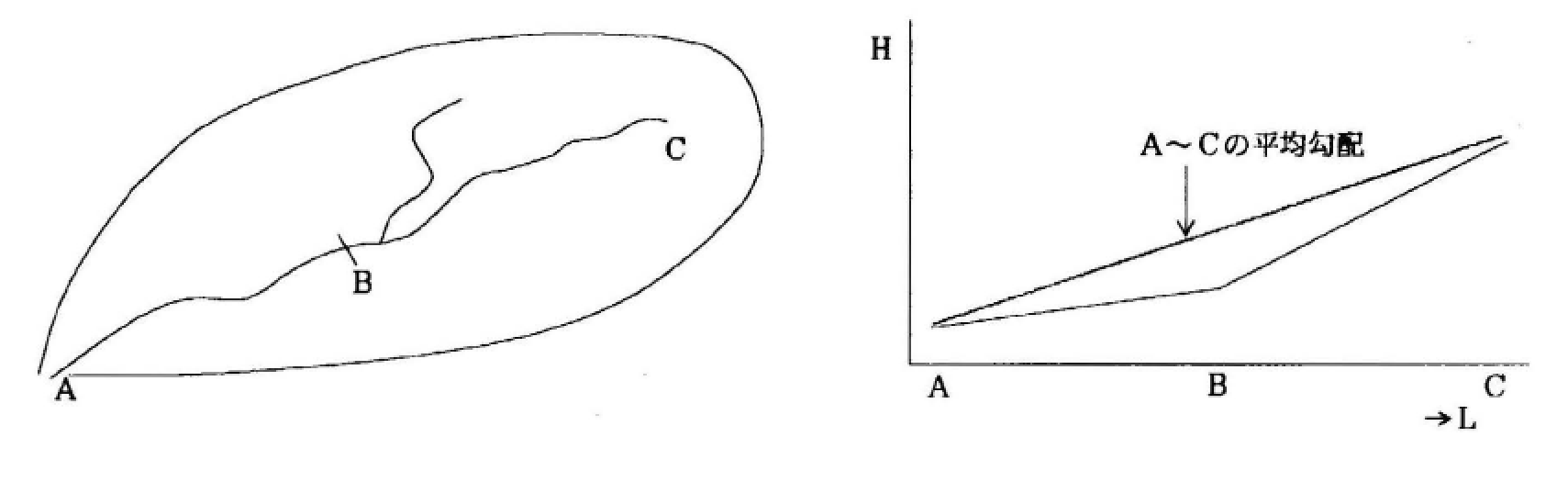
一般に河川は上流へいくほど勾配が急であることから、河道の縦断勾配の変化が大きい場合には、図に示すように適切な箇所に勾配変化点を設定し、区間毎に流路長、勾配を設定して、河道の流下時間を合算して求める。

A ～ C の平均勾配とすると勾配が全区間 1/100 以上となり流速を過大に見積もる恐れがある。

等流流速法

等流流速法は、クラーヘン式と同様に洪水到達時間を流入時間と河道流下時間の和で与える方法である。流入時間はクラーヘン式の場合と同じ値が用いられる。

河道流下時間はクラーヘン式の洪水伝播速度 W を以下のマニング式で求めるものである。

$$W = \frac{1}{n} R^{\frac{2}{3}} I^{\frac{1}{2}}$$

ここに、

• $W$：洪水伝播速度（m/s）
• $n$：河道の粗度係数
• $R$：河川代表断面の径深（m）$R=\frac{A}{S}$
• $I$：河床勾配

土研式

土研式は、土木研究所が全国の流出試験地等の水文データより、到達時間$T$($hr$)、流路延長$L$($m$)、流域勾配$S$の関係について整理し、導いたものである。

都市流域：$T = 2.40 \times 10^{-4} \left(\frac{L}{\sqrt{S}}\right)^{0.7}$

自然流域：$T = 1.67 \times 10^{-3} \left(\frac{L}{\sqrt{S}}\right)^{0.7}$

ここに、

• $L$：流域最遠点（流域界）から流量検討地点までの主流路の距離（m）
• $S$：流域最遠点（流域界）から流量検討地点の標高差を流路長（$L$）で割ったもの

ただし、土研式の適用範囲は、

• 都市流域で流域面積$A < 10\mathrm{km}^2$、$S > \frac{1}{300}$
• 自然流域で流域面積$A < 50\mathrm{km}^2$、$S > \frac{1}{300}$

なお、都市流域と自然流域が混在する場合は、100%都市流域、自然流域とした場合の洪水到達時間を面積加重平均より算定する。

$$T = \frac{A_T \times T_T + A_S \times T_S}{A_T + A_S}$$

ここに、

• $A_T$：都市流域面積
• $A_S$：自然流域面積
• $T_T$：100%都市流域とした場合の到達時間
• $T_S$：100%自然流域とした場合の到達時間

クラーヘン式と土研式

土研式は流出試験地等の水文資料より、計画上の安全側を見込んで、洪水遅れ時間実測値の下限値を採用し、それを 2 倍して洪水到達時間としている。吉野らによれば平均的には洪水到達時間は、クラーヘン式 > 土研式とされるが、勾配のとり方や流入時間の考え方等、本文で示した方法と異なることが考えられる。現実の計算例ではクラーヘン式による洪水到達時間は、土研式によるものよりも概ね小さ目を与えることが多い。

これらの式を使うにあたり、どちらが大きい流量を与えるかという点ではなく、流域の土地利用の変化をどのように予測し、河川計画を策定すべきかについて考える必要がある。すなわち、両者の特徴は以下のように示される。

1. クラーヘン式

   • 洪水到達時間に流域の土地利用の変化を表現することができない。土地利用変化は流出係数で表現するのみであるから、例えば原野からビルの密集した市街地に変化したとしても、流出係数は高々 0.7 から 0.9 に変化するだけで、計画高水流量は約 3 割しか増加しない。
   • 土地利用の動向は不明であるが、余裕をもって河川計画を策定したいときに適している。

2. 土研式

   • 流域の土地利用の変化を洪水到達時間と流出係数の 2 つのパラメータで表現することができるので、流域の特性を評価しやすい。
   • 将来の土地利用変化をある程度予測することができ、流域の特性を表現した合理的な河川計画を策定したいときに適している。 :::

流出係数

「建設省河川砂防技術基準(案) 計画編 p. 19」に記載されている以下の値を標準値とし、土地利用ごとの流出係数を用いて、当該河川の土地利用面積で加重平均し、流域平均の流出係数を設定する。

土地利用区分	流出係数
密集市街地	0.9
一般市街地	0.8
畑、原野	0.6
水田	0.7
山地	0.7

合理式の流出係数

合理式の流出係数は、総降雨量と総流出高の比である洪水の総流出率とは異なり、ピーク流量に寄与する到達時間内の降雨の流出率を示すものである。

一般に降雨流出過程においては、すべての降雨が洪水流出に寄与するのではなく、降雨初期には森林による降雨の遮断や葉面からの蒸発散、土壌中への浸透等によって流出に寄与する降雨（有効降雨）は比較的少ない。降雨が継続するにつれ、全降雨に占める有効降雨が増加し、流域が飽和した状態ではほとんどすべての降雨が流出に寄与するようになる。

以上のことを、総雨量と総損失量の関係で示したものが下図である。ある飽和点（図では山地で A 点、市街地で B 点）に達するまでは、雨量の増加とともに損失量も増加するが、飽和点に達した段階で損失量は一定に近くなり、すべての降雨が流出に寄与することとなる。

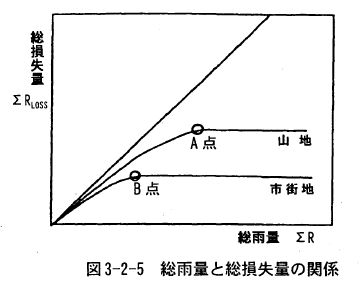
実際の洪水時には流域の湿潤状態や降雨量あるいは降雨強度により図の関係は変化する。また、地目による損失量が異なることから、流出係数は地目別に設定されている。

合理式における流出係数は、現実の降雨～流出機構が総雨量や降雨強度により変化するにもかかわらず、洪水ピーク時には流域が飽和に近い状態にあることを前提としている。従って、他の流出計算手法では前期降雨も含めてその外力となる降雨の計画規模を定めているのに対し、合理式では流域がある程度湿潤した状態で計画規模の降雨が生起した場合の流出量を算出しているため、他の流出計算手法に比べて大きめの流量が算出されることになる。流域が合理式自体の前提となる飽和状態に達していない場合には計画規模の降雨が生起したとしても、合理式で算出された流量は生起しない。このことが住民感覚との乖離を生む原因となっていると考えられる。これらのことから表に示した流出係数は、合理式自体の仮定に基づく種々の誤差を含んだ計画に用いる定数として扱うことが重要である。なお、全国流出試験地の資料を参考に吉野らが調べた結果によると、表に示したピーク流出係数$f_{p}$は、洪水の総流出率$F$に対し $f_{p}=(1.0~1.4)F$の関係が得られている。