河道計画
粗度係数の設定
粗度係数は、河道状況および対象とする洪水規模を踏まえ適切に設定する。
粗度係数は、水理量(水位・流速)に最も影響を与える要因の一つである。しかし、その値は一定値ではなく、河道状況(形状・河床材料・植生分布等)および洪水規模(水深)により変化し、様々な値をとる。そのため、河道計画においては河道状況および想定する洪水規模を踏まえ、適切な粗度係数を設定することが必要である。
特に、計画河道及び計画高水位を検討する場合は、改修直後の計画河道を想定して粗度係数を設定するのではなく、将来の維持管理状況をも考慮し、長期的な視点から粗度係数を設定する必要がある。
仮に標準断面(多自然型などを考慮しない場合)のみから粗度係数を設定した場合、粗度係数は実際の値よりも小さく設定され、下表に示すように治水上、危険側の計画となることがある。
| 検討項目 | 検討結果 | 想定規模の洪水が発生した場合 |
|---|---|---|
| 河道の断面設定 | 流下能力が過大評価されている | 危険 |
| 護岸等の施設設計 | 流速が大きく評価されている | 安全 |
| 遊水地等の越流量の算定 | 水位が低く算定され、越流量が過小評価されている | 遊水地は危険、河道は安全 |
拡幅・掘削等の河川改修を行うことにより、河床形状・河床材料等の河道特性が大きく変化する場合は、特に注意して粗度係数を適切に設定しなければならない。
粗度係数の設定方法としては、大きく分けて以下の 2 つの方法がある。
-
既往洪水データから逆算した粗度係数を設定(逆算粗度係数)
-
河床や護岸などの粗度状況から粗度係数を設定(合成粗度係数)
当該河川において洪水時に水位・流量観測、痕跡水位の測定が行われ、精度上、十分な量と質の実測データが存在する場合に、粗度係数を逆算から求めて設定する方法が採用できる。また、十分な実測データがない場合、もしくはデータが存在していても精度に問題がある場合において、河道の粗度状況(河床材料、植生、護岸等)を合成して粗度係数を設定する方法がある。
逆算粗度係数の長所は、実績データを用いるため、様々な要素による洪水流への影響が集約されていることである。一方、短所としては、逆算の対象�とする洪水と計画対象洪水の生起とでは河床の状況が大きく異なることがあるため、1 洪水のみで粗度係数を設定することはリスクを伴うことと、実績データの精度に大きく左右されることが挙げられる。
合成粗度係数の長所は、任意断面形状、洪水規模、粗度状況に適用でき、一般性、応用性が高いことである。短所としては、推定精度及び適用範囲に限界や不確定要素が残ること、土丹、岩河川に適用できないこと、河床材料の平面分布、鉛直分布にばらつきが大きい場合、一律に設定することが困難であることが挙げられる。
したがって一般的には、両者の欠点を補う形で 2 つの設定方法を併用し、粗度係数を適切に設定することが現実的な選択肢となる。つまり、以下の方法を取ることが望ましい。
-
河道の粗度状況から粗度係数を設定する一方で、その設定により既往代表洪水の逆算粗度係数あるいは洪水位を再現できるかを確認し、必要に応じて、設定粗度係数を修正する。
-
逆算粗度係数を設定することを試みる一方、逆算対象の洪水規模・河道状況と粗度係数設定対象のそれらとの違いを踏まえ、河床材料などの物理的な粗度係数を加味して、最終的に粗度係数を設定する。
粗度係数の設定区間
粗度係数は、各断面でそれぞれ設定するのではなく、河道区間を縦断的に河床材料、河床勾配、断面形状等により粗度係数がほぼ一定と考えられる区間に分�割して、その区間毎に設定する。その際、粗度係数を一律に設定する区間があまり短くならないように注意する。
逆算粗度係数の設定方法
河道の平均的な粗度係数を逆算する方法は、流量観測による実績流量と洪水後に測定される痕跡水位を用いて以下の手順で行う。
-
先ず、粗度係数を仮定して不等流計算を行い、得られた計算水位と痕跡水位とを比較する。
-
そして、その誤差が許容範囲内に収まるまで粗度係数を変化させて計算を行い、逆算対象洪水位を精度良く再現できた時の粗度係数を逆算粗度係数として設定する。
逆算に用いる痕跡水位の選定にあたっては、精度の高い痕跡を重視する。また、以下のような場合でも、それらがデータ的に同一の精度と考えられる限り、計算水位がそれらの平均値を通るように粗度係数を求めるものとする。
-
左右岸の痕跡水位が大きく異なるような場合
-
下流の痕跡水位が上流のそれよりも大きいような場合
詳しくは「建設省河川砂防技術基準(案)調査編、6.4 粗度係数の逆算法」を参照のこと。
合成粗度係数の設定方法
単断面河道における粗�度係数の設定方法は、中小河川では川幅水深比が小さく、側壁(護岸法面粗度)の影響が無視できないことを考慮し、断面を河床部と護岸部(法面部)に分けて粗度係数を設定し、これらを合成して求める。この合成粗度係数は、各部位毎の粗度係数とその潤辺により次式を用いて求める。
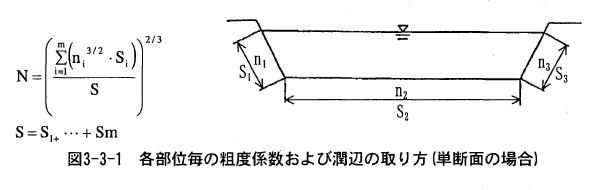
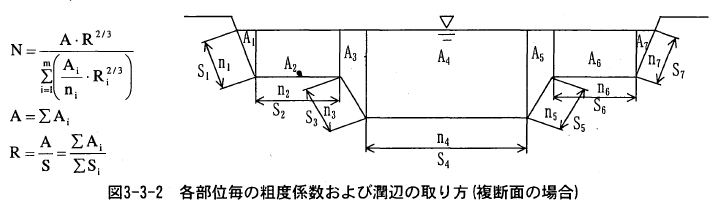
複断面河道の場合は、低水路、高水敷、護岸部に分けて粗度係数を設定しこれらを合成して求める。この式は、分割した断面間での流れの干渉(せん断力)を無視し、それぞれの断面で独立して流れが生じていると仮定して導かれたものである。
粗度係数の一般値
河道計画の策定に用いる粗度係数は、複断面等の横断形、河床形態、植生の状況等により適切に定めるものとする。 洪水時に水位·流量観測、痕跡水位の測定が行われ、精度上、十分な量と質の実測データが存在する場合に、粗度係数を逆算から求めて設定する方法を採用する。 改修前と後では河道条件が一変してしまい、かつ洪水資料がない場合には、十分な検討ができないことがあるので、単純な断面の河道では次の値を用いてもよい。
河道の種類 粗度係数の範囲 一般河道 0.030~0.035 急流河川および河幅が広く水深の浅い河川 0.040~0.050
建設省河川砂防技術基準(案)計画編
河道計画に用いる水位計算
河道の水位計算は、基本的に不等流計算を用いる。 また、複断面河道や樹木群の影響等を無視できない河道では、断面を分割して計算を行う準二次元不等流計算の適用についても検討する。
水位に影響を与える要素としては、主に表に示すような項目が挙げられる。表には、検討手法により考慮できるものとできないものを示している。
| 水位に影響を及ぼす要素 | 等流計算 | 不等流計算 |
|---|---|---|
| 断面形状 | ○ | ○ |
| 河床勾配 | ○ | ○ |
| 低水路·高水敷の粗度 | ○ | ○ |
| 滋一部の粗度 | ○ | ○ |
| 出発水位(河口、合流点水位) | × | ○ |
| 急拡·急縮等の断面変化 | × | ○ |
| 合流 | × | ○ |
| 河川構造物(橋脚·堰等) | × | ○ |
| 湾曲 | ○ | ○ |
| 砂州 | ○ | ○ |
| 植生 | ○ | ○ |
| 低水路と高水敷の流れの干渉 | ○ | ○ |
| 下(上)流の影響 | × | ○ |
なお、直轄の大河川ではこれらの項目のうち、ほぼ全てを必須項目として水位計算に取り込んで河道計画を策定しているが、中小河川では計算に必要な資料の制約もあることから、検討目的·計算手法により検討項目を適宜、選定することが望ましい。
一例として、河道形状が縦横断に変化する一般的な河道において、不等流計算と等流計算により得られる水位を比較した事例を図に示す。不等流計算では、任意地点の水位がその地点の下流断面における水位(射流では上流断面水位)から算出されるため、下(上)流水位の影響を適切に反映した連続的な水位を得ることができる。一方、等流計算では、各地点毎に水位が独立して得られるので、検討区間内に断面形状·河床勾配等の縦断的な変化や堰·橋脚等の河川構造物が存在する場合に、それらの影響範囲を評価することができない。
今後の川づくりでは、治水面だけでなく環境面にも配慮した河道計画、つまり一様な定規断面による河��道計画ではなく、現況河道形状を重視し、河道内樹木の存置による影響等をも考慮した河道計画を行う必要がある。また、流下能力の小さい中小河川では、橋脚や落差工等の構造物が水位に及ぼす影響も大きく、特に構造物設置地点より上流区間の堰上げを適切に考慮しなければならない。したがって、中小河川においても実際の水理現象の再現性が高く、精度良く水位を評価できる不等流計算を行うことが望ましい。
なお、水位に影響を及ぼす要素のうち、どの項目を考慮するかは、当該河川の規模及び重要度、沿川の土地利用状況等の諸条件を考慮し、適切に選定するものとする。
ただし、以下の場合については、等流計算により水位を算定することもできる。
-
急流河川で、常に射流が現れる
-
特に河川構造物もなく、横断面形及び河床勾配が変化しない
射流が現れる目安となる河床勾配は、フルード数の条件の下、マニング式より次式で求めることができる。
ここで、は河床勾配、は粗度係数、は径深、は重力加速度である。仮に粗度係数を、径深を、重力加速度をとすると、射流が現れる河床勾配は程度になる。
不等流計算は逐次不等流計算法を標準とするが、複断面河道で高水敷が広く、低水路流れと高水敷流れの相互干渉による抵抗の増加や樹木群の影響等を無視できない河道では、断面を分割して計算を行う準二次元不等流計算を用いる必要がある。計算方法は、「河川砂防技術基準(案)調査編」を参照のこと。
不等流計算式
流量一定で質量の保存則が成立する場合、不等流の運動方程式は図ー 5.5.2 に示す記号に従い、距離だけ離れた断面 I 及び II について差分形で表すと次式のようになる。
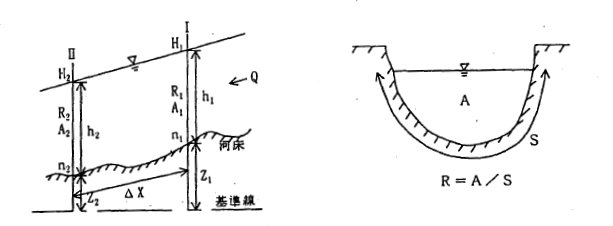
ここに、
- :流量
- :径深
- :水位
- :潤辺
- :水深
- :マニングの粗度係数
- :河床高
- :断面間距離
- :河積
エネルギー損失には、壁面のせん断力による損失(摩擦損失)の他に横断面形や縦断形状の急変によく生じる流線のねじれ、壁面からの剥離等に伴う損失(形状損失)があり、水位計算にはこれらの損失を適切に評価する必要がある。
- : 摩擦損失
- : 急拡・急縮による損失
- : 橋脚による損失(堰上げ)
- : 縦断形状の急変による損失
摩擦損失に関しては、抵抗則としてマニングの平均流速公式を用い、エネルギー式と同様に差分形で表した次式により算定する。
形状損失に関しては、急拡・急縮による損失は死水域の設定で、橋脚による損失及び縦断形状の急変による損失は、局所的な水位の変化量として把握する(「建設省河川砂防技術基準(案)調査編」参照)。
計算は、常流では下流側の条件の影響が上流に及ぶため、下流から上流に向かって行い、射流では逆に上流から下流に向かって行わなければならない。そのため、境界条件は流れが常流の場合にはその下流端水位(河口潮位、H~Q 曲線水位、支配断面水位)を、射流の場合には上流の支配断面水位を与える。
解法の手順としては、流れが常流の時には、境界条件として最下流端に水位(あるいは水深)を与え、距離だけ離れた断面 Ⅰ における水位(あるいは)を仮定して径深、河積を断面特性により求め、上式を用いて水位(あるいは)を計算する。これがさきに仮定したと異なる場合は、の仮定を修正して同様の計算を行い、計算値が仮定値と一致するまで繰り返し計算を行う。仮定したと計算したが一致すれば、このが断面 Ⅰ における水位であり、これが求まるとさらにだけ上流地点の水位を同様の方法で計算し、順次同じ手続きを繰り返し上流に計算していく。
流れが常流()の場合、任意地点の水面は流量と下流の水面とによって決定されるが、射流()の場合には下流の水面には関係なく、上流側の水面高によって決定される。そのため、常流と射流が混在する区間においては、流れの状態によって不等流計算を行う方向が異なるので注意を要する。
実際に計算を行う際には、フルード数によるチェックを行い、支配断面の有無を確認しておく必要がある。そして、必要に応じて内挿断面を挿入し不等流計算を行う。
詳しくは「建設省河川砂防技術基準(案)調査編、参考 6.12.1 支配断面が現れる場合」を参照のこと。
等流計算式
近似的に流れが等流と見なせる場合、以下に示す摩擦損失のみを考慮したマニングの平均流速公式と連続式を用いて水位を算定する。
ここで、近似的に等流と見なせる流れとは、堰・橋脚等の河川構造物の影響が及ばない区間、断面形状の変化が小さい区間での流れが相当する。
ここで、
- :平均流速(m/s)
- :粗度係数
- :径深(m)
- :エネルギー勾配
- :流量(m³/s)
- :流水断面積(m²)
等流計算の場合、エネルギー勾配は、河床勾配で置き換えることができる。
また、径深は潤辺長(m)を用いて次式で算定する。
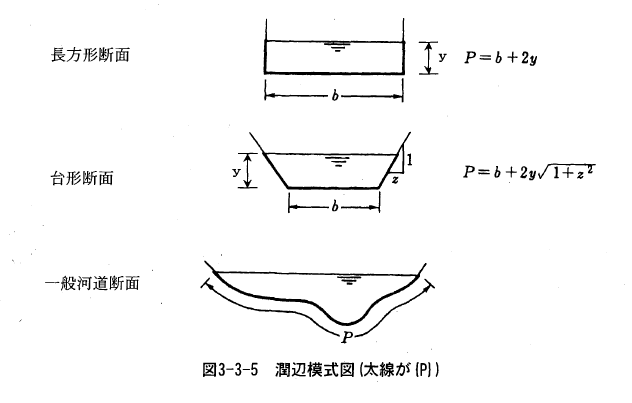
河底幅、護岸の勾配(1:2.0、図 3-3-5 の台形断面参照)、水路勾配、粗度係数のとき、等流状態での水深における等流流量を計算する。
流水面積:
潤辺:
径深:
平均流速:
等流流量:
なお、以上の水理諸量は、とすれば長方形断面のそれになる。
計算例 1 の水路が等流流量を流している。等流水深を計算する。
等流流量は連続式のにマニング式を代入することにより与えられるから、これに、、、、の各値を代入すると、
となり、トライアル&エラーで右辺がほぼ左辺に等しくなるの値を求める。
等流水深()